I- THEORIE DE LA MUSIQUE

1- L’ECHELLE MUSICALE

C’est une suite de sons, appelés notes, présentés sous forme de degrés d’une échelle. Ces sons/notes (ainsi que d’autres) sont employés pour faire de la musique : composer, jouer ou chanter. Cette échelle commence par une note grave (càd de basse fréquence) appelée tonique. Les notes suivantes deviennent de plus en plus aigues, et se terminent par l’octave qui résonne en complète “harmonie” avec la tonique. Nous reviendrons plus loin (IV) sur les raisons acoustiques qui ont abouti au choix de ces notes, leur nombre et leur hauteur (pitch chez les anglo-saxons).
L’échelle de base contient 7 notes/degrés, leurs noms sont Do-Ré-Mi-Fa-Sol-La-Si (-Do), chez les anglo-saxons : C-D-E-F-G-A-B (-C). Ce sont les touches blanches du clavier du piano. Les degrés de cette échelle de base ne sont pas égaux. Si nous considérons l’intervalle entre Do et Ré comme unité, exprimée par “ton”, entre chaque note et la suivante (par exemple Do-Ré ou Ré-Mi ou Fa-Sol), la distance est un ton entier, à l’exception de Mi-Fa et Si-Do qui sont seulement d’un demi-ton (2 figures suivantes).

Cette échelle heptatonique est la référence, mais il y a des peuples qui utilisent une échelle pentatonique, en enlevant les demi-tons (Mi et Si). D’un autre coté, il y a aussi des divisions de l’octave en 12, 19, 24 “degrés” (et même plus).
Les notes de musique et de chant sont exprimées au moyen de plusieurs lignes parallèles groupées en 2 ensembles appelés “portée”, marquée chacune par un signe particulier à gauche. La plus répandue est désignée par “Clé de Sol”. Ainsi vous pouvez voir les tons et demi-tons à l’intérieur d’une octave (on peut les étendre en haut et en bas) :

Le schéma du clavier montre comment diviser chacun des 5 tons ( Do-Ré, Ré-Mi, Fa-Sol, Sol-La, La-Si) en insérant une touche noire, il en résulte que l’étendue globale d’une octave est 12 degrés de demi-tons. Parmi ces 12 degrés seulement 7 au maximum sont pris pour créer une mélodie, il forment alors un “mode” (ou une gamme), ou une “tonalité” (terme lié au système “tonal”, càd le style pratiqué depuis fin 17^ème siècle, avec une dominance des accords II).
La note Do en dessous de la clé de Sol (ligne supplémentaire) correspond à la touche Do du milieu du clavier, et les notes supérieures couvrent (en gros) les touches de la moitié droite. Pour les touches de la moitié gauche, et généralement pour les voix/sons graves, un 2^ème ensemble de lignes parallèles commence par cette note Do et s’étend vers le bas, c'est la clé de Fa :

2- MODES DIATONIQUES/NATURELS

Partout dans le monde, une mélodie n’utilise jamais n’importe quels sons (càd n’importe quelles fréquences) parmi les sons infinis disponibles dans la nature, mais seulement certains sons dont le nombre ne dépasse pas 7, disposés selon un schéma/modèle précis appelé “mode” (ou gamme). Nous allons commencer par les 7 sons diatoniques/naturels, touches blanches du piano.
Le premier et le plus largement répandu (en Occident) est calqué sur l’échelle, et est alors considéré comme référence ou modèle, c’est l’ionien (ou mode de Do), avec T = ton entier et ½ = demi-ton :

Nous pouvons observer que la distance/intervalle de la quinte vaut 3 tons et demi (3 ½ ) et est qualifiée de juste (ou parfaite), et la tierce de 2 tons est qualifiée de majeure.
Le second “mode” est le mineur (naturel, antique) ou éolien (mode de La), il est défini par la suite des 7 notes commençant par la note La :

La quinte La-Mi vaut toujours 3 tons et demi, elle est donc juste/parfaite (comme en mode majeur) mais la tierce La-Do avec seulement 1 ton et demi est mineure. Pour des raisons liées à l’Harmonie (II) le 7^ème degré est élevé d’un demi-ton, le mode est alors qualifié de “mineur harmonique”.
Ce sont là les 2 modes officiels de la culture occidentale, hérités de la Renaissance, et transmis au continent américain et au reste du monde. Cependant il existe un 3^ème mode ayant une faible présence (chez les allemands protestants et russes orthodoxes), c’est le phrygien ou mode de Mi (maqam kourde d’Orient), par exemple la cantate de Bach “Aus tiefer Not schrei ich zu dir” :

Ainsi, on peut former ou concevoir 7 modes contenant seulement les touches diatoniques blanches (ils étaient tous utilisés à differents degrés jusqu’à la fin de la Renaissance), partant d’une note quelconque : Do (ionien), Ré (dorien), Mi (phrygien), …La (éolien). Le locrien Si était peu utilisé à cause de sa quinte de seulement 3 tons ( ½ 1 1 ½ 1 1 1 ).

3- MODES CHROMATIQUES

En divisant chaque ton en 2 nous obtenons 5 nouvelles notes (touches noires), on ne leur a pas donné de nouveaux noms mais on les désigne au moyen de signes de 2 sortes : dièse # pour élever la note d’un demi-ton, et bémol b pour baisser la note d’un demi-ton. Ainsi les 5 touches noires sont :
Do# = Réb , Ré#= Mib et Fa# = Solb , Sol# = Lab , La# = Sib
Si, pour une raison quelconque, on veut commencer un mode majeur par Sol, une quinte plus haut, toutes les notes vont être rehaussées d’un intervalle de 3 tons et demi, il faudrait apporter une alteration/correction aux notes de l’échelle de base :

On a été amené à élever Fa au moyen du signe # . Essayez de faire la même chose, en partant de Fa, il sera néceassaire de baisser Si d’un bémol b :

Si on veut former un mode mineur commençant par Ré ou Mi (en respectant le modèle de La) on sera amené a bémoliser Si (en Ré mineur) ou diéser Fa (en Mi mineur).
Les alterations qui affectent certaines notes dans le but de modifier la forme/structure et de définir le mode sont groupées à gauche, juste après la clé (Sol ou Fa) et désignées par le terme armure ou armature. Un 3^ème signe sert à annuler l’effet des dièses et bémols, c’est le bécarre : ♮

Remarque : Un mode particulier, le Hijaz (½  3/2   ½   T   ½   T   T), assez présent en Orient, il était utilisé en Espagne mauresque, et est toujours utilisé en Espagne. Il porte plusieurs noms : tzigane, andalous ou arabo-andalous, spanish gypsy, freygish, spanish phrygian, phrygien dominant, Bhairavi indien ou Ahava Rabbah chez les juifs :

Armure/Armature Si on prend n’importe laquelle des sept (ou douze) notes comme tonique, quelles sont les alterations qu’il faut apporter pour obtenir un mode majeur ou mineur. Par exemple, quelle est l’armure de Sol mineur? La réponse est : deux bémols, Si et Mi. La méthode logique consiste à appliquer l’idée expliquée ci-haut, càd copier le modèle, mais cela demande à chaque fois une reflexion et un calcul qu’on peut éviter. Cette même methode conduit à une suite de dièses et bémols, il suffit de la retenir par coeur dans les 2 sens :

Le « Cercle des Quintes » (voir Remarque, fin de §4) donne un schéma circulaire de cette suite. On reviendra souvent sur ce Cercle

Ceci permet de dresser un double-tableau de modes majeurs et mineurs :

Explication, d’après ce double-tableau : Mib majeur : 3 bémols, Ré majeur : 2 dièses, Do mineur : 3 bémols, Si mineur : 2 dièses
Quant au phrygien, partant du mode mineur on doit baisser le second degré d’un demi-ton. Par exemple Sol mineur contient 2 bémols, Sib et Mib, on ajoute le bémol suivant Lab. Ainsi, l’armure de Sol phrygien est composé des 3 bémols, Sib-Mib-Lab.
Les 2 modes situés sur la même colonne ont la même armure : Sol majeur et Mi mineur avec 1 dièse, Fa majeur et Ré mineur avec 1 bémol, cela veut dire qu’ils utilisent exactement les mêmes 7 notes parmi les 12 disponibles, ils s’appellent “modes relatifs”.
Nous nous sommes arrêtés dans ce double-tableau au nombre de 5 altérations, mais plusieurs auteurs (et quelques compositeurs du 19^ème siècle) vont jusqu’à 6 ou 7, alors que presque tout le répertoire classique et moderne ne dépasse guère 3 ou 4 altérations.

4- LES INTERVALLES

Un intervalle est la distance entre 2 notes, souvent il a un qualificatif qui indique sa taille (le nombre de tons qu’il contient). Le tableau suivant montre les intervalles et leur distance à la tonique :

Pour deux notes quelconques X et Y, par exemple Ré et Si, il faut compter de X=1, …. jusqu’à Y : Ré =1, donc Si= 6, c’est une sixième, elle est majeure puisque sa distance est 4 tons et demi, alors que Mi-Do avec 4 tons est une sixième mineure. On peut étendre cette définition aux notes extérieures à l’octave.
L’octave : 6 tons. La quarte : 2 tons et demi, la quinte : 3 tons et demi (dans les 2 modes majeur ou mineur). Ces 3 degrés sont qualifiés de justes ou parfaits (P), parce que leur distance ne dépend pas du type de mode. Quant au reste des degrés, leur distance dépend du type de mode, et au lieu d’ être juste/parfait ils sont majeurs (M), mineurs (m), augmentés (A/aug) ou diminués (d/dim). L’augmenté a 1/2 ton plus que le parfait (exemple Do-Sol#) ou le majeur (Do-Mi#), le diminué a un 1/2 ton moins que le parfait (Do-Fab) ou le mineur (Mi-Solb).
Pour identifier un intervalle, les alterations sont d’abord ignorées : Ré-Si, Réb-Si, Ré#-Si, Ré#-Sib, sont tous des sixièmes même si leurs valeurs sont différentes. Do-Fa# est une quarte augmentée et Do-Solb est une quinte diminuée alors que leur valeur commune est 3 tons, c’est le fameux triton (diabolus).

Inversion : un intervalle X-Y peut être inversé/renversé pour devenir Y-X. Si la distance de X-Y est n (par exemple Ré-Si, une sixte), la distance de Y-X est m tq n+m = 9 ou m = 9-n (Si-Ré est une tierce). Après inversion/renversement, majeur devient mineur et vice versa (de même pour dim et aug, et parfait reste parfait).

La division en cents
Le Ton standard/égal (exacte sixième partie de l’octave) du clavier moderne (ou de la guitare avec frettes) est pris comme unité d’intervalle dans la pratique musicale (modes, solfège, accords). Quant aux théoriciens et autres musicologues qui étudient différents accordages et des intervalles non-standards il existe une autre unité, le cent qui vaut la centième partie du demi-ton standard : 1 demi-ton = 100 cents
Selon cette definition, l’octave vaut 1200 cents, la quarte 500 et la quinte 700, dans le temperament égal (ET, Equal Tuning)

Rapport d’intervalle
Depuis les temps anciens, les théoriciens (et autres spéculateurs [Th, pp7-11]) exprimaient les intervalles au moyen de rapports/ fractions. Au début, c’était appliqué à un instrument archaique ayant une seule corde : le monocorde, ou canon. Le terme canon signifie modèle ou référence qui sert à faire des mesures. Les “philosophes” grecs de l’Antiquité ont étudié le monocorde, leur objectif était de le diviser pour créer plusieurs sons, mais cet objectif n’était pas realisé car leur unique instrument la lyre (à la différence du violon ou de la guitare) était composé de cordes isolés non divisibles.
Prenons une corde de 60 cm, en posant le doigt de la main gauche à différents endroits on diminue la partie vibrante et on joue les notes de l’échelle : Do (à vide), Ré, Mi, Fa, Sol, etc (voir plus bas). Essayez de jouer le Do suivant, càd l’octave, et mesurez la longueur de la partie vibrante, vous trouverez 30cm. Le rapport entre 60 et 30 est 60/30 = 2/1 = 2 . Essayez de jouer la quinte Sol, sa position est située à 20 cm du sillet, la partie vibrante est de 40cm et le rapport est alors 60/40 = 3/2 (ou 1,5). Pour la quarte Fa ce sera 45 cm et le rapport 60/45 = 4/3 . Pour le reste des notes, vous trouverez une série de fractions dont les valeurs sont comprises de 1 et 2 , et peuvent être exprimées sous forme de nombres décimaux : le son devient aigu et la fréquence (pitch dans le jargon musical) augmente jusqu’à devenir double (détails en III).

Le concept de rapport/fraction nous permet d’étudier les intervalles du point de vue arithmétique, càd l’addition et la soustraction d’intervalles. Par exemple, on va faire la somme d’une quinte 3/2 et d’une quarte 4/3 (Do→Sol et Sol→Do suivant). Vue la nature scientifique des intervalles (III.2), on doit appliquer une multiplication et non pas une addition. Ce n’est pas correct d’écrire “3/2 + 4/3” et ceci ne donnera pas une octave (3/2 + 4/3 = 17/6 ≈ 3 >> 2), l’opération correcte est
3/2 × 4/3 = 4/2 = 2
Quinte + quarte = octave
Ajouter des intervalles dans le cas mentionné ci-dessus est facile et conduit à de simples fractions (de nombres entiers), mais dans d’autres cas (l’octave contient 12 intervalles) ça peut être difficile à réaliser. Pour cette raison, les théoriciens ont élaboré la division en “cents”.

Remarque : Ce concept suppose que la quinte est de 3/2 = 1,5 = 1,5000 (et la quarte est 4/3 = 1,3333), alors que les quintes dans le clavier moderne sont 1,4983 (détails en III.2) et ceci est la valeur exacte utilisée dans le Cercle des Quintes §3 et dans le Tableau de la division en “cents” ci-dessus, c’est 3/2 moins (-) 1/12 de comma (IV).
A ce stade cette Remarque peut vous sembler dérisoire ou insignifiante, mais elle vous aidera à comprendre le chapitre IV.

5- QUART-DE-TON ET MICRO-TONALITE

Des degrés (ou intervalles) plus petits que le demi-ton ont existé depuis la Grèce antique. Ils ont été éliminés par le moine bénédictin D’Arezzo (en l’an 1000 environ) dans ses écrits mais ils sont restés dans la pratique jusqu’au 13^ème siècle. Des novateurs (comme Nicola Vicentino) ont essayé de les relancer au 16^ème siècle mais depuis D’Arezzo la théorie était régie par une structure semi-tonale. Une échelle à 19 divisions par octave a été conçue au 16^ème siècle et a survécu jusqu’au 17^ème (IV.4), elle équivaut au Système de 1/3 de ton. Le quart de ton va apparaitre au début du 20^ème siècle en relation avec la Micro-Tonalité (ultra-chromatisme) moderne [Th, pp200-204] : Alois Haba, Wyschnegradsky, Georgy Rimsky-Korsakov (“The Basis of the Quarter-Tone Musical System”, 1925), etc. http://electro-music.com/forum/topic-20747.html , https://en.wikipedia.org/wiki/Microtonal_music.
Le quart de ton est présent dans la musique orientale. On trouve rarement un quart de ton isolé, et presque toujours il sert pour former de nouveaux intervalles non existant dans l’échelle occidentale, en particulier ¾ de ton. Il est désigné par 2 signes derivés des altérations standards : Demi-dièse ≠ , similaire au dièse avec un seul trai vertical, il élève la note d’un quart-de-ton . Ce signe est utilisé depuis les années 1970 dans la “musique spectrale” quand des compositeurs ont remarqué la présence de Fa≠ dans la série des harmoniques (II.2 et III.5). Demi-bémol, il se présente sous différents aspects derivés du bémol, le plus courant est un bémol barré, il baisse la note d’un quart-de-ton .
Le Rast est en quelque sorte une référence ou un modèle pour les modes orientaux, il peut être considéré comme un compromis entre le majeur et le mineur (avec T = 1 ton et ¾ = ¾ de ton) :

On trouve ce mode dans les chants afro-américains de Blues et de Gospel, un mode “tempéré” qui évite les demi-tons.
Les musiques orientales (arabe, perse, turque, byzantine, indienne) emploient de nombreux modes (maqams ou maqamat), ils n’ont pas été imposés par des théoriciens (comme en Europe) mais ont été élaborés et ont évolué pendant des siècles grâce à de grands virtuoses. Leurs origines sont d’anciennes mélodies créées par des musiciens, entretenues et améliorées par des générations jusqu’à être gravées dans la mémoire collective, et finalement adoptées par les théoriciens. Alors qu’en Occident les théoriciens de la Renaissance avaient décrété la suprématie du seul mode majeur, suivi par le mineur au début du Baroque.
Il y a plusieurs dizaines de modes orientaux, exploités en Proche et Moyen-Orient et en Afrique du Nord, mais pas au même degré. Rast et Bayate sont les plus courants, d’autres sont rares. Pour celà on devrait les ranger dans 3 classes : les plus courants sont environ 10 ( voir tableau plus bas), suit une autre liste d’une douzaine présente dans le grand répertoire accessible à la plupart des musiciens, et une vingtaine connue seulement des grands professionnels et des musicologues. Le problème est que certains de ces modes ont des genres (5 premières notes) similaires ou le même tétracorde puisque la quinte est habituellement parfaite (3 tons et demi). Ainsi, il est préférable de compter les genres plutôt que les modes (pour les modes indiens voir [Th, p167]).

6- ACCORDS ET TRIADES

“Triade” est un ancien terme qui a été progressivement remplacé par “accord” lequel contient une idée de consonnance et d’harmonie (bien qu’il existe des accords non consonants). La forme basique d’un accord est un ensemble de 3 notes superposées, càd exécutées simultanément (en position verticale sur la portée) : tonique/racine/fondamental, tierce et quinte parfaite, exemple : Do-Mi-Sol ou La-Do-Mi. Le premier est majeur puisque sa tierce (Do-Mi, 2 tons) est majeure, le second avec une tierce mineure (La-Do, 1 ton et demi) est mineur. Dans ces 2 cas, l’accord est qualifié de parfait. L’accord diminué, ayant 2 tierces mineures, est moins fréquent : Si-Ré-Fa.

Ces suites sont conformes au modèle 1-3-5, mais dans la pratique elles peuvent être modifiées : en ajoutant l’octave, supprimant ou déplaçant la tierce, ou plus généralement en posant les 3 notes n’importe comment à condition que la tonique (Do) reste à la basse (état fondamental ou position initiale) :

Parfois l’accord admet une 4^ème note (1-3-5-7 : accord de 7^ème ) ou même une 5^ème (1-3-5-7-9 : accord de 9^ème ), ceci donne de nombreux accords dont voici les plus courants (avec Dom = dominante) :

Do-Mi, Mi-Sol, Sol-Sib , Sib -Ré, c’est une succession de tierces (majeures et mineures). Cette forme fait dire aux musiclogues qu’un accord est une suite de tierces (pseudo-règle des tierces superposées, tertial/tertian Harmony chez les anglo-saxons). Ce point de vue est absolument faux, et ne repose sur aucun argument acoustique.
Depuis l’avènement des triades au début de la Renaissance (vers 1400), le but était de superposer des notes censées être consonantes avec la racine quand elles sont exécutées ensemble (II.2-3), ce sont les harmoniques de la racine. Le problème est que l’évolution de la musique à travers les siècles a conduit à tenir compte de plusieurs accords dissonants (ils jouent un “rôle” dans la composition, ils doivent être résolus).

Renversement
En écrivant les différentes lignes ou les accords en Harmonie Classique (II), les compositeurs baroques étaient souvent amenés à “inverser” l’accord, càd changer l’ordre direct 1-3-5 et la racine n’est plus à la basse. Cet acte permet plus de choix dans les notes à placer sur chaque ligne; en d’autres termes le “renversement” n’à aucun motif esthétique, c’est seulement un moyen pragmatique pour l’écriture à plusieurs voix.

La forme obtenue n’est plus conforme à la triade 1-3-5, càd une note basse, sa tierce et sa quinte. Ainsi, d’autres intervalles, comme la 4te et la 6te apparaissent et ne sont pas harmonieux. Rameau a écrit sur “l’aspect scientifique” des accords, il a prétendu que malgré celà on peut entendre la racine mais ceci est faut (détails dans [Ac, pp172-173]).

Chiffrage/ Notation
En Classique et dans la plupart des musique modernes, les accords sont exprimés par l’écriture des notes qu’ils contiennent, comme les exemples ci-dessus et celui de II.1, il suffit donc d’exécuter les notes écrites sur la portée. D’autres notations existent, elles évitent l’écriture de toutes les notes, et laissent certaine liberté aux exécutants.

La vieille notation baroque (toujours en usage) consiste à poser le fondamental (c’est la racine des américains) et compléter par des chiffres pour indiquer l’état ou la “qualité” de l’accord (état initial ou nième inversion, majeur ou mineur …), exemple en II.4.

Quelques notations baroques :

En notation moderne (d’origine américaine) on pose la racine et on ajoute des signes/lettres qui indiquent la “qualité” des accords. Ainsi si la racine est R : R majuscule (ou RM, ou Rmaj) pour le majeur, r minuscule (ou Rm ou Rmin) pour le mineur, etc :

Si on est dans une tonalité déterminée, Do majeur par exemple, les accords peuvent être exprimés selon leur rang par des chiffres romains : lettres majuscules pour le majeur et minuscules pour le mineur:

Une autre notation est utilisée par des partitions modernes, particulièrement en jazz, et supposée simplifier la lecture, mais elle est équivalente à la notation baroque : Sol7 = accord de dominante de Sol en état fondamental, Do/Mi = Do majeur en 1^er renversement (Mi est à la basse), Fa/Mi = accord de Fa 7^ème en 3^ème renversement (Mi est à la basse).

II- HARMONIE ET CONTREPOINT

1- INTRODUCTION

La partition ci-dessous présente une composition moderne pour piano, dans le style harmonique classique (un passage simplifié de “Le Lac” par S. Donval). On peut observer 2 portées : une mélodie (chant) en clé de Sol interprétée par la main droite, et en clé de Fa une suite d’accords Fa-Do-Fa (I-V-I). On peut voir/traiter cette pièce des points de vue Harmonie ou Contrepoint :

L’Harmonie est l’art ou la technique de combiner plusieurs lignes/voix, ou ajouter des accords à un theme. Il s’git ici de “l’Harmonie Tonale”, telle qu’elle est pratiquée depuis la période baroque (plus précisément depuis fin 17^ème siècle), exploitant seulement les 2 modes majeur/ionien et mineur/éolien, plus de détails en §4-5.
Auparavant (Moyen-Age tardif et Renaissance), la musique savante était dominée par la Polyphonie qui a connu son apogée au 16ème siècle. La Polyphonie est un ensemble de 3 ou 4 (ou plus) lignes mélodiques qui doivent respecter un nombre de règles relevant du Contrepoint. La ligne d’en haut (chant ou main droite du clavecin, clé de Sol) devenait imposante et les autres lignes d’en bas étaient groupées en clé de Fa. Plus tard, elles ont été réduites à une seule ligne présentant les accords : Basse Chiffrée §4. L’Harmonie a évolué progressivement durant 3 siècles environ pour devenir le style classique (et ensuite moderne) de la musique occidentale, où la progression des accords est un facteur dominant. Pendant toute cette évolution, la relation entre notes verticales a été une affaire de Consonance §3, régie par les lois de l’Acoustique (dans le sens Physique, III et [Ac]), comme on va le voir dans le prochain chapitre sur “l’Acoustique Musicale”

2- LES HARMONIQUES

Les instruments de musique sont nombreux et différents, et chacun a son propre sonorité et une intonation spécifique (timbre). Qu’est ce qui fait que ces sonorités soient si différentes? La réponse est qu’il n’y a aucun “corps sonore” (corde, tube, caisse) qui donne un son ayant une fréquence précise et unique. Le principal son (III) est toujours accompagné par une série de sons secondaires d’amplitudes/intensités plus faibles, leurs fréquences sont multiples de celle du son principal. Ce sont les harmoniques (partials ou overtones chez les anglo-saxons) et sont responsables de la différence entre sonorités. Ils sont aussi responsables de la Consonance qui est au coeur de la Musique et sa Théorie et Harmonie.
Prenons une note dont la fréquence est, par exemple, 100 Hz . N’importe quel instrument qui produit cette note va émettre aussi des sons de (en plus de 100 Hz) : 200, 300, 400, 500, 600, 700, etc, Hz. Ce phenomène est inhérent à la Nature. L’oreille perçoit la combinaison de tous ces harmoniques, ils varient selon la “source acoustique”, sinon tout le monde aura la même voix et tous les instruments de musique donneront la même sonorité.
Si on considère Do1 (2^ème ligne supplémentaire sous la clé de Fa), ses harmoniques couvrent entièrement les 2 clés, et deviennent très proches vers l’aigu. Ils sont disponibles dans tous les cours de Théorie et d’Harmonie. Le problème est que dans tous ces écrits le 11^ème harmonique est présenté par Fa ou Fa# , alors qu’en réalité il se situe au milieu de ces 2 notes et il est désigné par Fa ≠ ( le signe ≠ est un demi-dièse). La figure suivante montre les harmoniques successifs de Do1 : Do2, Sol2, Do3, Mi3, Sol3, Sib3, Do4, etc.

Certains de ces harmoniques (une fois ramenés à l’intérieur de l’octave) coincident avec les degrés de l’échelle, en particulier l’octave et la quinte. Un autre peut être grossièrement comparé à la tierce majeure, d’autres sont moins proches (Sib3) ou un peu loins (Lab4) de leurs correspondants. La raison est que l’échelle occidentale moderne a dévié du principe qui est à l’origine de sa construction pendant la Renaissance (IV), et lequel devait respecter les critères de consonance.
Les rapports de ces harmoniques avec le fondamental sont : 2, 3, 4, 5, 6, 7, etc. et sont situés au-dessus de l’octave. Si on veut les ramener à l’intérieur de l’octave on doit les diviser par 2 (une ou plusieurs fois) pour avoir un rapport entre 1 (tonique) et 2 (octave). Le résultat est : 2/1, 3/2, 5/4, 7/4, etc. Ils représentent, dans l’ordre : l’octave, la quinte, la tierce juste/parfaite, la 7^ème harmonique.
Le plus important degré de l’échelle, après la tonique et l’octave, est la quinte/dominante, nous la trouvons dans tous les accords (comme en cadence finale). Vient ensuite la tierce, qui créa de nombreux problèmes dans l’histoire de la musique. Diviser l’échelle en degrés égaux (de 100 cents pour chaque demi-ton) n’est pas justifié du point de vue musical (IV.4-5). Cela aboutit à une tierce majeure de 400 cents, plus haute que la tierce juste/pure 5/4 de 386 cents (formule dans III.2). Cette tierce pure a été le noyau de la théorie musicale depuis la Renaissance parce qu’elle offre un accord très harmonieux (IV). Et pour cette raison, la division de l’échelle en 19 degrés (au lieu de 12) au 17^ème siècle était instaurée, mais elle n’a pas pu survivre car le clavier devenait complexe et l’idée était abandonee (pour la même raison, Ourmaoui, théoricien du 13ème siècle a conçu une échelle à 17 degrés dont la principale caractéristique était une tierce pure en usage au Moyen-Orient jusqu’au 19^ème siècle quand elle a été découverte par Villoteau qui accompagnait Napoléon en Egypte [Th, p137-p201]).

3- CONSONANCE ET ACCORDS

Tous les musiciens à travers le Monde appliquent le principe de la Consonance sans y prêter attention. Quand un violoniste ou un guitariste veut accorder une corde il la compare à son octave ou à sa quinte, parce qu'il y a une (très) agréable sensation avec ces 2 intervalles, ce phénomène s’appelle “Consonance”, l’opposé est Dissonance. L’explication scientifique (III) est que ces notes sont les premières et les plus fortes parmi les harmoniques de la tonique ([Ac,VII]).
Il y a unanimité sur la consonance de ces 2 degrés, dans l’ordre, l’octave et la quinte. Elles ont toujours été dans l’accord depuis son apparition, et depuis le début de la Renaissance (environ 1400) les chants polyphoniques étaient terminés par les 3 notes : tonique, quinte, octave (la tierce arrivera plus tard).
Ces notes sont à l’intérieur de l’octave mais il y en a plusieurs autres au-dessus de l’octave qui sont consonantes et qu’on peut trouver facilement. On doit utiliser alors un clavier de piano et partir d’une note très basse (extrême gauche du clavier) : pressons en continu le Do le plus bas.Il y a principalement 2 séries de notes consonantes : le Do suivant et ses octaves successives, la dominante Sol et ses octaves successives. Si on suppose que la fréquence de la tonique est 100 Hz, parmi ses harmoniques §2 :
* 200, 400, 800 … sont les octaves (1ème, 2ème, 3ème …), puisqu’à chaque fois la fréquence (ou le rapport) est doublée.
* 300 est le douzième degré ou l’octave de la dominante, 600 et 1200 sont ses (première et seconde) octaves. Si on veut retrouver la quinte/dominante, sa fréquence est 300 ÷ 2 = 150 ; son rapport est 150/100 = 3/2 = 1,5 .
* Quant à 500, il indique un son très proche du 17^ème degré, localisé 2 octaves au-dessus de la tierce. En descendant d’une octave on obtient la dixième 500/2 = 250, en descendant d’une autre octave on obtient la tierce 250/2 = 1,25 = 5/4 . Le problème est que ce rapport correspond à 386 cents et diffère de la tierce majeure (1,2656 ou 400 cents, IV.2) de l’échelle à division égale (ET, equal Tuning/ Temperament) actuellement en usage dans la musique occidentale. La difference est faible (moins d’un comma, IV) mais son impact est significatif, comme nous allons voir plus loin.
L’accord, depuis son ancêtre la triade, a été écrit sous la forme de série de tierces superposées (dans sa position initiale dite fondamentale), à tel point que la plupart des gens pensent que c’est celà sa définition (Chailley : pseudo règle des tierces superposées). Ceci est erroné car l’idée fondatrice de l’accord est la Consonance.
Ce qui ajoute à la confusion est le phenomène de Renversement, très exploité en Occident pour des raisons qui n’ont rien à voir avec la musicalité, l’intonation ou la perception. Il mène à des accords dissonants, avec des quartes et des sixtes, appelés accords artificiels (par comparaison aux accords naturels ayant seulement des tierces et des quintes).
Les intervalles d’octave et de quinte, sont reconnus comme les plus consonants par les praticiens aussi bien que par les théoriciens, mais l’erreur commise par les théoriciens du Moyen-Age tardif a été d’inclure la quarte dans la série des consonances. Les responsables de cette erreur ne sont pas les musiciens mais les théoriciens qui étaient des moines/ecclesiastiques partisans de 1-4-5 et qui ont rarement touché à un instrument. Au 14^ème siècle, les compositeurs ont commencé à se conformer à des critères esthétiques/ acoustiques en utilisant des triades 1-3-5. La 4te a gardé son importance (avec la 5te) instaurée par le moine bénédictin D’Arezzo 3 siècles auparavant et restée ancrée dans la Tradition. Ça donnera plus tard la clé de Fa. Une autre raison est que la quarte, avec la tonique et la quinte, sont les racines des accords majeurs alors que le reste des degrés sont mineurs.
Remarque : les harmoniques dont parlaient les anciens théoriciens, pendant 2 millénaires, ente -300 et +1700 n’ont rien à voir avec les fréquences multiples.

4- L’HARMONIE

La musique occidentale (classique, moderne, jazz, variétés) est harmonique, contrairement à d’autres musiques (surtout orientales) qui sont mélodiques, càd elles contiennent une seule ligne/voix (la musique mélodique a toujours existé en Europe de l’Ouest depuis le 12^ème siècle chez les Troubadours mais n’a pas été suffisamment mise en valeur par les auteurs [Th, pp65-68]). La présence des accords (et leur hiérarchie) est presque aussi importante que la mélodie. Le “mode” s’appelle alors “tonalité”, par opposition à la “modalité” de la Renaissance.
Par définition, l’Harmonie est l’art ou la technique de composer des oeuvres contenant plusieurs lignes/voix superposées et l’usage des accords dans le but d’assurer une meilleure intonation. Apparue au 17^ème siècle, elle est la conséquence de l’évolution du Contrepoint (15^ème et 16^ème) qui était la technique de combiner des mélodies indépendantes et était appliqué à la Polyphonie de la Renaissance.
Bien qu’il y ait plusieurs différences entre les deux, Contrepoint et Harmonie sont 2 étapes de l’évolution de la composition. Le premier consistait à créer une mélodie et ajouter d’autres voix en respectant la consonance selon l’ancienne croyance (degrés 1,4,5), on utilisait les anciens modes, et les musicologues qualifient ce style de “modal”. Quant au second, le style tonal harmonique exploite les accords, leur marche/progression, et leur variation pour avoir l’aternance entre consonants (stables, avec calme et repos) et dissonants (instables, avec tension).
L’accord de tonique est omniprésent dans toute la phrase, souvent précédé par l’accord de dominante (comme en cadence §5); la phrase doit commencer et finir par l’accord de tonique dans son Etat Fondamental. Ces 2 accords, tonique et quinte, sont les plus importants en composition, et leur présence définit la tonalité.
La première phase de l’Harmonie est la “Basse Chiffrée” (début 17^ème siècle), elle a évolué à partir de la Polyphonie de la Renaissance (et la technique du Contrepoint) en fusionnant les lignes d’en bas dans la clé de Fa alors que la mélodie est restée en clé de Sol, c’était destiné aux joueurs de clavecin et luth. La ligne basse s’est transformée progressivement en série d’accords, chaque accord est identifié par une note sous laquelle est écrite la notation de “Basse Chiffrée” : un ou deux (parfois trois) chiffres verticaux : 5sur3 (ou seulement 5) pour l’Etat Fondamental, 6sur3 (ou seulement 6) pour le premier Renversement. Le compositeur indique seulement la nature et la qualité de l’accord, par exemple Accord de Dominante Sol en second Renversement (Sol, Si, Ré avec Ré à la basse) : G +6, alors l’exécutant va improviser à sa convenance, càd il va jouer ces notes dans n’importe quelle position sur la portée, à condition que Ré reste à la basse. Un exemple de Couperin, 1700 :

Remarque : Le système “tonal” classique favorise les 3 accords I, V, IV; c’est une tradition qui date d’un millénaire quand D’Arezzo a institué la suprématie de ces 3 degrés (appelés “notes tonales”), mais IV est tombé à un niveau plus bas (avec d’autres degrés).

5- REGLES D’HARMONIE

Dès le début de la Renaissance la triade 1-3-5 a été pleinement adoptée par les musiciens et les théoriciens de la Polyphonie. Il n’y avait pas de thème dans la ligne supérieure comme aujourd’hui, l’écriture consistait à superposer des lignes mélodiques indépendantes. Leur nombre varie : 2, 3 ou plus mais la norme est 4 dont les noms de bas haut sont : Basse, Tenor, Alto, Soprano, chacune a son propre ambitus/ tessiture :

Au départ, on commençait souvent par la ligne du bas ou “teneur”. Teneur signifie pillier, ou quelque chose qui tient/porte l’ensemble de l’oeuvre, il dérive du verbe latin “tenir”. C’était le “Cantus Firmus” des anciens auteurs, sous forme d’un chant simple avec des notes lentes/longues.
Pendant la Renaissance (16^ème siècle), cette structure a évolué graduellement pour se concentrer sur l’esthétique dans la ligne supérieure à la manière des chansons de trouvères. Après une courte période de Basse Chiffrée (17^ème), les compositeurs ont préféré la notion d’accord, employant aussi des accords dissonants dans le but d’avoir l’alternance et une meilleure intonation. Le résultat de cette évolution est l’avènement d’un nouveau style appelée “Mélodie Accompagnée”. Ce style, qui a survécu jusqu’à nos jours, domine l’orchestre philharmonique et le jeu du piano : un thème qu’il soit vocal ou instrumental en haut (clé de Sol) et les accords ou l’accompagnement en bas (clé de Fa), et les notes verticales sur le même battement de mesure doivent appartenir au même accord.
Cette forme basée sur des lignes indépendantes était instaurée par des auteurs rigoristes, mais en pratique plusieurs compositeurs ont posé la ligne supérieure (mélodie) suivie de 2 (ou 3) lignes d’accompagnement. Cette technique était répandue surtout en musique profane (De La Halle 13^ème, Landini 14^ème) mais les musicologistes l’ont toujours négligée .

Remarque : Pour une meilleure intonation, le mouvement parallèle est strictement interdit pour les octaves et les quintes parce que ces 2 intervalles sont les plus consonnants, et leur succession pourrait mener à une monotonie (remarquez qu’on a ignoré la quarte).

Progression d’accords
Les règles d’Harmonie ci-dessous concernent toutes les oeuvres de musique/chant ployphonique depuis fin 17^ème, utilisant seulement le majeur et le mineur harmonique, mettant en exergue les accords et leur progression. L’alternance est recommandée, entre accords stables/calmes (qui marquent la tonalité) I et V (plus IV, parfois) d’un coté, et accords instables/tendus (ou renversés) de degrés tels que II et VI de l’autre. La présence de III et VII est plutôt faible. On ne peut pas donner une entière argumentation pour justifier toutes ces notions car l’Harmonie a évolué le long des siècles selon la pratique, la tradition et le gout.
Contrairement au Contrepoint, le rȏle des accords est important, et ils ne sont pas posés n’importe comment, il y a des séries appelées prgressions (ou marches harmoniques) : la plus simple est (I-) V- I , la plus courante en style classique est (I-) IV - V- I . Plusieurs progressions ont été utilisées dans l’Histoire selon la période, la région ou le style, l’une des plus répandues en musique moderne est I-V-VI-IV, comme dans “Let it be” (https://en.wikipedia.org/wiki/List_of_songs_containing_the_I–V–vi–IV_progression).

Résolution
C’est le mouvement d’un accord dissonant (ou tension) à un accord consonnant (calme/quiétude). La Résolution signifie résoudre une situation difficile / non satisfaisante. Elle obéit à des conditions qu’on trouve dans tous les cours d’Harmonie. Elle peut avoir lieu dans plusieurs situations (dissonance, inversion, degrés/ accords faibles) : on doit passer à une “situation stable” càd l’accord de tonique (directement ou à travers la dominante) en position initiale/fondamentale (voir Note Sensible et Cadence).
L’inversion crée une vraie confusion : des accords consonants (I, V ou n’importe) une fois renversés ne sont plus consonants, puisqu’ils contiennent des intervalles autres que la tierce et la quinte (en Do majeur : 4te Sol-Do, 6te Sol-Mi), on doit donc les résoudre.

Note Sensible
Une mélodie/monodie finit toujours par la tonique précédée de notes conjointes, parfois par l’octave précédée de la septième (ou la dominante) qui se trouve à un demi-ton en-dessous. Ceci est dû à des arguments acoustiques que nous expliquons en détail dans la section acoustique (battements de 2 sons III.4), ils recommendent de monter d’un demi-ton (ou descendre d’un ton, une variation de fréquence de 10% au maximum qui élimine les battements). Pour cette raison, la septième mineure (5 tons) est rehaussée par un dièse pour être proche de l’octave : cette proximité d’un demi-ton crée une “attraction” vers l’octave qui offre une situation stable.
Quant à la musique harmonique, on a besoin de ce fait d’élever la 7^ème mineure pour former la cadence parfaite, sorte de Résolution qui termine une phrase. Si le mode est La mineur, on rehausse Sol vers Sol# pour avoir l’accord Mi-Sol#-Si-Ré 1-3-5-7 sur la dominante (accord de 7^ème de dominante) qui précède l’accord parfait de tonique (voir exemple plus bas).
Dans les 2 cas on aboutit au mineur harmonique.

Cadence
La monotonie ne répond pas aux attentes de l’esthétique, et une phrase doit contenir des étapes de calme/quiétude et de tension, et des pauses/arrêts de différentes longueurs pour diviser la phrase comme les points et virgules dans un texte littéral. On appelle ces pauses “cadences”, elles sont précédées de courtes marches harmoniques qui contribuent à l’Intonation. Il y en a 4 ou 5 sortes, leurs noms/adjectifs varient légèrement selon les auteurs. La plus importante est la cadence parfaite/authentique, elle est la cause de la création du mineur harmonique. Elle marque un arrêt définitif de la phrase : accord parfait 1-3-5 en position initiale, précédé de l’accord parfait 1-3-5 (ou 7^ème 1-3-5-7) de dominante (voir exemple).
Parfois, pour finir un passage (ou pour une raison quelconque), le compositeur décide un arrêt temporaire; il peut invertir l’accord de tonique. Dans ce cas, la cadence ne donne pas une sensation d’arrêt long/ définitif parce que la note basse n’est pas la tonique, c’est une cadence imparfaite. La cadence plagale consiste en une succession des accords IV et I, le dernier en position initiale; avec IV à la place de V cette cadence est moins pertinente que la parfaite (plagale signifie fausse, non authentique).
Il y a au moins une autre sorte de cadence qui finit par la dominante, en position initiale, elle s’appelle demi-cadence.
Seule la cadence parfaite convient pour un arrêt définitif du point de vue acoustique (les autres sont valables, elles ont été instaurées par la Tradition et des considérations esthétiques). Voici 2 exemples de cadence parfaite :
En Do majeur on a Do (I) : Do-Mi-Sol et Sol (V): Sol-Si-Ré (ou Sol-Si-Ré-Fa). Le passage de V vers I doit être conjoint pour toutes les notes (à l’exception de Sol→Do), la raison est due à des critères acoustiques [Ac, chap XIX] :
Si → Do, montée d’un demi-ton, obligatoire, ça permet d’éliminer les battements (III.4)
Ré → Do ou Mi, mouvement d’un ton, reposant
Sol → Do, à la basse, clé de Fa (Sol peut rester en place en clé de Sol)
Fa → Mi, en cas de 7^ème de dominante

La Modulation
Une oeuvre musicale est rarement écrite en un mode unique, à moins qu’elle soit très courte. La mélodie principale (ou thème) est composée dans un mode donné, mais très souvent on change de mode. Le nouveau mode est très proche du mode principal, et le changement est appelé “Modulation”. La modulation est faite pour des besoins d’Esthétique et d’Intonation.
Le second thème est écrit dans un mode relatif (I.3). Il peut commencer par la dominante (ou la sous-dominante moins souvent), ainsi on rajoute une altération. De toutes façons, le changement doit obéir à certaines conditions, et d’habitude il passe à un mode voisin, qui diffère au maximum par 2 altérations : d’abord vers le mode relatif (avec la même armure), ensuite vers la quinte ou la quarte (et leurs modes relatifs) avec une altéraion en plus. Finalement, on a jouté (ou supprimé) 1 ou 2 altérations (en tenant compte de la sensible). Il est aussi possible de passer du majeur vers le mineur (ou vice-versa), cela implique 2 altérations en plus (“Jeux Interdits”, Narciso Yepes).

III- ACOUSTIQUE MUSICALE

1- INTRODUCTION

Ce chapitre traite les principes acoustiques qui expliquent les règles de base de la théorie musicale : échelle, accords (renversement, résolution), l’Harmonie et les harmoniques, etc.
Tout d’abord, pourquoi l’échelle musicale est composée de 7 degrés disposés selon un modèle rigide (I.1)? Pourquoi l’Occident exploite seulement 2 modes, le majeur et le mineur, parmi les 7 disponibles. Pouquoi les européens de l’Ouest ont abandonné le quart de ton et autres micro-tons utilisés par les anciens grecs et qui ont survécu jusqu’à la Renaissance?
Depuis environ 2 siècles et demi, la division de l’échelle musicale a été égalisée, càd tous les 12 demi-tons (diatoniques aussi bien que chromatiques) ont eu la même hauteur (exacte douzième partie de l’octave, ou 100 cents, I.4) alors qu’ils étaient légèrement inégaux dans la période baroque. C’est le Tempérament (accordage) Egal (standard), des théoriciens l’appellent “accordage tempéré” (il y a nuance entre les 2 termes). Le Tempérament Egal moderne est le résultat de la simplification des tempéraments du Baroque, et de l’avis de presque tout le monde il n’est pas convenable. La raison est qu’il n’offre pas d’accords harmonieux du fait de la (mauvaise) qualité de ses tierces majeures (la tierce harmonique est la plus consonante, elle est plus basse d’un comma, neuvième de ton IV). C’est pour cela qu’il y a eu à la Renaissance plusieurs tentatives de concevoir des Tempéraments avec des tierces consonantes; le plus connu est celui de Zarlino mais le mésotonique (IV) a eu plus de succès. Quant à la quinte, sa consonance (II.3) a toujours été acceptée comme excellente.
La Consonance est le facteur commun entre l’Acoustique et la Théorie Musicale, elle est la preuve que toutes les musiques du monde (occidentale, orientale, indienne, chinoise, etc.) sont basées sur les mêmes lois acoustiques (au sens physique du terme). Elle est aussi le fondement des accords puisque ceux-ci sont supposés être composés de notes harmonieuses, et par conséquent c’est le concept essentiel de l’Harmonie : tous les degrés d’un accord sont dérivés des harmoniques de la basse/racine (excepté le 11^ème, sans parler du 13^ème). Quant au renversement, il n’a aucune justification musicale; il conduit à des accords dissonants (qui sont exploités pour créer l’alternance et l’intonation).
La théorie musicale occidentale est très influencée par la culture catholique car elle était dominée par des moines et des ecclesiatiques, qui faisaient de la “musica speculativa” [Th, pp7-11] ancien nom de la théorie musicale, ils ont décrété des règles que les musiciens devaient appliquer. Nombre de ces règles n’étaient pas conformes aux critères acoustiques, on doit donc reconnaitre que la musique occidentale n’a rien d’universel. Notre but est justement de faire une analyse acoustique la plus objective de la musique.

2- MESURE D’INTERVALLES

Depuis l’Antiquité on a établi une équivalence reliant les intervalles de musique et les rapports de longueurs (rapports de longueurs de cordes, ou de distances entre les trous d’un instrument à vent). Les positions de l’octave, la quinte et la quarte sont dans l’ordre à 1/2, 1/3 et 1/4 de la longueur totale de la corde, à partir du sillet (figure dans I.4). A l’aide d’une règle graduée on peut facilement mesurer le rapport entre 2 positions et ainsi déduire la hauteur de l’intervalle des 2 notes.
Le problème est que jusqu’au 17^ème siècle on ignorait la nature du son et la notion de fréquence : le son est l’effet de la vibration d’une corde (ou n’importe quel autre corps sonore) sur l’oreille, àprès transmission à travers l’air. Si une longueur l donne un son de fréquence f, une longueur l’ donnera un son dont la fréquence f’ est telle que :

Par comparaison à la corde à vide, on peut constater que les parties vibrantes de la quarte, la quinte et l’octave sont : 3/4, 2/3, 1/2 ; alors les rapports de leurs fréquences sont : 4/3, 3/2, 2 et sont compris entre les valeurs 1 et 2 : Plus la fréquence augmente, plus la longueur diminue et plus le son devient aigu.

Fonction Logarithme
L’usage de la fonction logarithme n’est pas indispensable, on peut l’éviter et utiliser seulement les rapports de fréquences, mais la division en cents fournit une graduation linéaire/ régulière de l’échelle de fréquences. Bien qu’elle ne soit pas difficile à manipuler, sa présence peut impressionner des gens qui ne sont pas supposés avoir une formation scientifique, sa principale caractéristique : log(a×b) = log(a)+log(b) pour 2 nombres a et b quelconques.
Il est commode de lire des quantités qui s’ajoutent plutôt des quantités qui se multiplient, mais la nature de certaines grandeurs comme le son (ou l’intensité sonore) les rend non additives, ainsi le Bel et le déciBel ont été définis par une fonction logarithme. L’intervalle (exprimé par un rapport de fréquences) lui aussi n’est pas une grandeur additive, on fait alors appel à la fonction logarithme.
Un exemple concret, quarte : log(4/3)=0,124939 et quinte : log(3/2)=0,176091 , dans ce cas il s’agit de log décimal ou log₁₀ . La somme de 0,124939+0,176091 = 0,30103 n’est autre que log(2) et “2” c’est l’octave.
Il est facile de déterminer la valeur en cents d’un intervalle d’après son rapport, en utilisant la formule ci-dessous. Pour le ET (I.4) on peut trouver la valeur des 7 ou 12 degrés sans passer par cette formule. Avec l’hypothèse que tous les demi-tons sont égaux à 100 cents, on doit calculer x tel que x¹² = 2 , ce nombre x est la racine 12^ème de 2 : ¹²√2 = 2^1/12 = 1,0594631 (pour un ton entier 1,0594631² = 1,12246). En d’autres termes, si vous multipliez ce nombre "x" 12 fois par lui-même (ce qui équivaut à ajouter 12 fois le même intervalle de demi-ton) vous trouverez "2" .

La précision est de 5 décimaux, il est évident que ce n’est pas utile pour le praticien mais c’est nécessaire quand on doit faire plusieurs opérations théoriques successives. A propos, veuillez comparer ces rapports de Fa et Sol avec ceux à la fin de I.4.

Formule de graduation (en cents)
Prenons un exemple réel : Fa et Si; leurs rapports sont : "F"=1,3348, "B"=1,8877 . Leur distance est 1,8877÷1,3348 = 1,4142 , càd le rapport f’/f de leur fréquences (ou l’inverse de leurs longueurs vibrantes) est 1,4142 . Quelle est la fréquence de leur milieu ? Ce n’est pas la moyenne (dans le sens arithmétique) ( f + f’ ) / 2 = ( f + 1,4142 f ) / 2 = 1,2071 × f = 1,6112 mais on va voir plus loin que c’est √( f x f’) = 1,5874 (="Sol#"="Lab"). Un autre exemple similaire : 4te + 5te = 8ve , la relation entre leurs 3 rapports est 4/3 × 3/2 = 12/6 = 2 , la difference 3/2 ÷ 4/3 = 9/8 (204 cents) est un ton (pythagorien). Ainsi la graduation de l’échelle de fréquences doit se faire d’une manière multiplicative/ logarithmique (et non additive/ linéaire ).
Les théoriciens n’aiment pas employer l’unité “fréquence”. Au lieu d’exprimer l’étendue d’un intervalle entre 2 notes par le rapport de leurs fréquences, ils ont employé l’unité “savart” présente dans plusieurs traités jusqu’au milieu 20^ème siècle, mais écartée par le “cent”. Le cent est conçu de telle sorte que le demi-ton égal/standard (diatonique ou chromatique), qui est l’exacte 12^ème partie de l’octave, soit égal à 100 cents. C’est une unité simple et claire, commode et largement adoptée de nos jours :
I (f,f’) = 1200 × log₂ (f’/f)
Cette formule divise l’étendue d’une octave (de 1 à 2) en parties égales/ régulières de "1" si f’=f (0 cent) à "2" si f’ = 2×f (1200 cents).

3- UN PEU D’HISTOIRE

La première citation dans l’Europe Antique du concept des rapports de longueurs et leur relation avec les intervalles est mentionnée dans le livre “Division du monocorde” ou “Division du Canon”, attribué à Euclide (vers 300 A.-J.). Le vrai auteur est Cleonides, beaucoup moins connu qu’Euclides mais il y a une petite similitude entre les 2 noms. Un monocorde a servi comme modèle (canon) pour étudier et déterminer les rapports de longueurs et par la suite concevoir une soit-disant échelle musicale. Le polymathe gréco-romain du 2^ème siècle Ptolemé a écrit ses “Harmoniques”, ce terme n’a rien à voir avec les harmoniques/ partiels mais décrit l’harmonicité du son et de la vue, et insiste sur les rapports de petits nombres pour expliquer la consonance. Bothèce (vers 500) à la fin de l’antiquité romaine était partisan des rapports superparticuliers de la forme : (n+1)/n = 1 + 1/n (3/2, 4/3, 5/4, 6/5, 7/6, …). Bien que la théorie des rapports simples ait survécu jusqu’à nos jours, nous sommes surs qu’elle n’a aucune relation avec la consonance [Ac, VII].
Le Moyen-Age est la période qui dure environ un millénaire, à partir de la chute de l’Empire Romain (en 476), mais la fin n’est pas très claire et généralement varie lelong de la seconde moitié du 15^ème siècle. Contrairement à l’Antiquité le M-A était une période de décadence et d’ignorance. D’Arezzo (vers l’an 1000) “a réduit tout au diatonique et a donné le coup de grâce au quart de ton hérité de la mélodie grecque” (Amédée Gastoué, Encyclopédie de la Musique, M-A, p559) et a conçu sa théorie de “l’Hexacorde”. En 1324-25, le Pape Jean 22 édita sa décrétale qui précéonisait l’usage de la quarte et la quinte comme meilleures consonnances (au lieu de la tierce et la quinte, qui mènent vers la triade 1-3-5).
La Renaissance est un grand tournant dans la théorie musicale. Grace à l’Hymne de Ramos de Pareja [Th, p100], l’avènement de l’octave remplace le vieux formalisme de l’Hexacorde. Malgré quelques tentatives comme celles de Francesco Salinas et de Nicola Vicentino, les théoriciens abandonnent les micro-tons, et décrètent la suprématie du mode majeur (qui est une copie de l’échelle). Plus tard, le mineur revient après l’admission de la consonance de la tierce mineure [Th, pp123-125].
L’accord de dominante apparaît au début du Baroque, le passage vers l’accord de tonique permet d’éliminer les “Battements” (§4) et répond donc à un besoin acoustique (Résoluton). A la même époque, la division de l’octave en 19 a eu du succès et nombreux claviers à 19 touches étaient fabriqués (IV.4).
Durant le “Siècle des Lumières”, les savants ont apporté de nouvelles et rigoureuses idées pour remédier aux failles inhérentes à la construction de l’échelle musicale. Ils se sont focalisés sur l’aspect acoustique des notes de musique et ont introduit d’autres degrés consonants pour améliorer l’Intonation Juste (IV). En 1700 Ch. Huygens a conçu une division à 31 tons [Ac, pp104-109] incluant le 7^ème harmonique (présent dans l’accord de 7^ème). Le français J. Sauveur (1653-1716) a mis en exergue qu’un son quelconque contient plusieurs partiels (overtones) : un son “pur” n’existe presque jamais. La principale onde est toujours accompagnée par d’autres ondes dont les fréquences sont multiples appelés harmoniques. Leur relative intensité (amplitude) donne des timbres variés et ainsi fait la différence entre instruments (et voix). Plus tard, Joseph Fourier (1768-1830) prouve mathématiquement qu’un signal périodique (tel qu’une vibration sonore) est la combinaison d’une série de fonctions sinus.
J. Ph. Rameau (1683-1764) est l’un des rares parmi les grands compositeurs qui ont essayé d’expliquer l’Harmonie sur des bases scientifiques bien qu’il ne soit pas un savant. Il était influencé par Sauveur et a écrit plusieurs traités pour exposer ses idées sur l’Harmonie et les accords [Ac, pp172-173].
F. Savart (1791-1841), un autre savant français avec un intérêt particulier pour les instruments de musique, inventa un appareil pour mesurer la fréquence du son, le sonomètre. Son nom a été affecté à une unité d’intervalle tombée en desuétude.
Le polymathe allemand H. von Helmholtz (1821-1894) a étudié le phénomène de “résonance” de sons complexes. Il anlysa l’effet des harmoniques sur la Consonance (§5) mais, malgré ses longues formules, il trouva des résultats déjà connus (peut-être avait-il l’intention de les justifier).
De nos jours, la conviction unanime est que les degrés consonants sont les plus proches harmoniques, mais il y a encore des gens qui croient que la quarte 4/3 (et même la tierce mineure 6/5) est un harmonique de la tonique, ceci est faux (§6).

4- ONDE SONORE ET FREQUENCE

Un exemple d’onde est ce qu’on voit à la surface d’une eau calme quand elle reçoit un jet de pierre : des ondes sont créées et propagées à partir du point d’impact dans toutes les directions. Le son est très similaire, avec l’air à la place de l’eau, mais ses ondes ne sont pas visibles.
Le son est la sensation produite par les vibrations d’un milieu matériel (air, eau de mer) sur l’oreille, le tympan reçoit les vibrations et les transmet au cerveau pour analyse (un “micro” opère d’une manière similaire). Ses caractéristiques sont :
* amplitude/ magnitude (loudness) : qui indique l’intensité, en Electronique le niveau sonore est évalué par une unité appelée le “Bel” ou “déciBel”, l’oreille humain supporte des sons (ou bruits) jusqu’à une centaine de dB.
* la fréquence : c’est le nombre d’ondes émises en une seconde, son unité officielle adoptée par les scientifiques est le Hertz, ou “cycle par seconde”. Plus le son est aigu et plus sa fréquence est grande, la bande maximale de sons audibles ne dépasse pas 20-20.000 Hz (infra et ultra-sons sont trop graves ou trop aigus pour l’oreille humaine). La bande 40-4000 (ne pas oublier les harmoniques) couvre les 7 octaves du piano.
* Le timbre est lié à la complexité de la forme de l’ondulation : un son “pur” a une courbe sinusoidale (fig 1) et ce n’est pas agréable à entendre, il ressemble à un sifflement. Un son réel est composé d’un fondamental et d’une série de sons partiels appelés harmoniques (spectre sonore, selon le jargon scientifique) avec des intensités plus ou moins faibles, et c’est cela qui fait la distinction entre les timbres.

Forme sinusoidale
La courbe de la fonction sinus est présentée en Mathématiques par figue 1 :

L’axe vertical des ordonnées indique l’amplitude (ou magnitude) “a” de la fonction sinus, et l’axe horizontal des abscisses le temps “t”.
Si vous regardez la surface de l’eau, perturbée par un jet de pierre, le long d’un rayon à un instant donné (imaginez que vous prenez une photo d’ensemble) vous verrez exactement une forme sinusoidale. Par ailleurs, si vous observez un point fixe, matérialisé par un petit objet flottant, il va monter et descendre, sa position varie dans le temps en décrivant une forme sinusoidale.
Il est évident qu’une vibration acoustique dépend à la fois du temps et de l’espace. Dans le but de simplifier gardons seulement le paramètre temps, l’amplitude de la vibration peut alors être exprimée en fonction du temps par a = A sin (2Лf × t). “A” est l’amplitude maximale.
La fréquence est le nombre de cycles/ondes par seconde. Quand on dit qu’un son a une fréquence de 100 Hz, ceci signifie que les ondes successives envoyées par la corde grattée atteignent le tympan 100 fois chaque seconde.
La durée d’une ondulation est T = 1s / 100 = 0.01s = 10 ms , c’est la période T de l’onde :

Par définition, un signal ou quoi que ce soit est dit périodique (ou cyclique) s’il se répète, identique à lui-même, régulièrement, après chaque intervalle de temps invariable que nous appelons période (il y a plusieurs exemples dans la Nature et la vie quotidienne ).
Les anciens théoriciens se sont toujours reférés à la longueur de corde pour étudier l’échelle musicale puisque les instruments à cordes étaient les plus largement utilisés et la mesure de la longueur est très aisée, alors que les instruments électriques/électroniques [Ac, XV-XVI] sont apparus il y a un siècle (Thérémine). Le facteur commun à tous ces dispositifs n’est pas la longueur mais la fréquence (Diapason La3 est déterminé par sa fréquence 440 Hz).

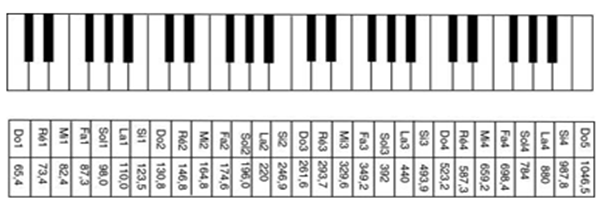
Fréquences des octaves centrales du clavier du piano (ET, Equal/Standard Temperament, [Ac, p16])

Le Battement de 2 sons
Le Battement est un phénomène qui survient quand 2 sons de fréquences très proches sont exécutés simultanément, et se présente sous forme de “fluctuations” d’amplitude.
La courbe n°1 est l’ “image” d’un son pur au sens physique/acoustique, elle est lisse et régulière. Un son quelconque a une courbe grossièrement similaire mais déformée, graphe n°2. Deux notes différentes, Do et Sol par exemple, donnent un son de courbe assez régulière, avec comme fondamental la fréquence de Do, puisque c’est un intervalle consonant. Autrement, le son résultant serait complexe et son image serait brouillée.
Dans le cas de 2 sons purs de fréquences f et f’ très proches (écart inférieur à 10% , càd f < f ’ < 1,1×f ), le son résultant a une fréquence entre f et f’ mais on peut entendre quelque chose qui ressemble à un son grave ayant une amplitude variable (des hauts et des bas). Ce sont des “Battements” (interférences), et cette expérience est facile à réaliser au moyen de 2 instruments pas bien accordés (d’ailleurs cela aide à les accorder) ou entre 2 notes voisines (essayer Do et Do# d’un clavier). Essayons d’accorder les cordes d’un violon sur la base d’une référence n°1 (La3, 440 Hz). Pour Mi4 n°2 aigue on doit trouver son enharmonique sur la corde référence, à une longueur de 1/3 à partir du sillet, cela laisse 2/3 de corde vibrante pour Mi. Le musicien va serrer ou desserer la Mi4, écoutant/ scrutant des battements jusqu’à ce que les 2 cordes soient bien accordées, et les battements sont éliminés.
D’anciens auteurs appellent cela “Son Différentiel” parce que sa fréquence est la différence entre f et f’. On peut prouver l’existence de ce “différentiel” par des formules mathématiques qui nécessitent des connaissances en fonctions sinusoidales ([Ac, pp199-201]): le résultat est un son unique, modulé en amplitude, de fréquence (f+f’)/2. Pendant longtemps la nature du “différentiel” a été débattue : Helmholtz était convaincu que c’était un son réel alors que Rameau pensait que c’était une simple illusion et il avait plutôt raison.

Son contre Bruit
Dans les dernières décennies, des musiciens novateurs ont commencé à exploiter le “Bruit” dans leurs œuvres, mais c’est quoi la différence entre “son” et “bruit” ?
N’importe quel signal émis par un corps sonore, s’il est court, peut durer une fraction de seconde, un dixième de seconde (0,1s) par exemple.Dans le cas du diapason de 440 Hz, la durée de chaque vibration, ou période T, est T = 1/f = 1/440 = 2,273 10^-3 s = 2,273 ms ≈ 2,3 ms. En conclusion, puisque 0,1s / 2,3ms ≈ 44, ce signal contient plusieurs dizaines d’ondes (sinus).
Ce qu’on appelle “bruit” est une suite de sons désordonnés, créés par un appareil qui n’est pas, a priori, destiné à émettre des sons, et il est donc de nature (intrinsèque) indésirable. Mais si on prend l’une des composantes de ce bruit, et qui dure une petite fraction de seconde, rien ne la distingue d’un signal créé par un piano ou un violon (excéptée la différence de timbre). La distinction se situe uniquement au niveau psychologique.
Un “bruit” et un son musical sont composés de signaux de même nature (càd vibrations acoustiques, avec harmoniques), sauf que dans un cas ces signaux sont arrangés selon le désir du musicien et sont interprétés par un instrument créé pour cette tâche, alors que dans l’autre cas ils sont désorganisés, et surtout founis par une machine qui n’appartient pas à l’orchestre. Le plus surprenant est que vous pouvez faire du bruit avec un piano, en tapant des notes disparates et incohérentes, non reliés entre elles, vous verrez la réaction de votre entourage.

5- LES HARMONIQUES

Consonance

Nous avons déjà expliqué cette notion en II.3 : Deux notes sont consonantes si elles créent une sensation d’harmonie (on dit aussi euphonie) et de détente/quiétude quand elles sont exécutées en même temps; une phrase finit toujours par une consonance (réalisée par un accord parfait dans son Etat Fondamental). Il n’y a pas de définition physique ou de formule mathématique pour exprimer cette notion, mais certains degrés de l’échelle ont été estimés comme consonants, et divers classements ont été faits depuis plusieurs siècles. C’est là l’origine des accords et de leur évolution dans l’Histoire.
L’octave est une parfaite consonance. La sensation créée par l’octave est due au fait que sa fréquence est double de celle de la tonique, et qu’elle est son plus proche harmonique, c’est le 2^ème après la tonique. Le son résultant a la tonique comme fondamental et l’octave ne fait que renforcer l’harmonique et modifie légèrement le timbre. La quinte produit un effet semblable mais à un degré moindre, puisque c’est le 3^ème harmonique, et a toujours été classée en second rang après l’octave. Ces 2 intervalles sont qualifiés de parfaits (justes chez les anglo-saxons).
Ensuite, historiquement vient la quarte bien que son cas soit très controversé, et la plupart des auteurs pensent (et écrivent) que c’est un harmonique, mais c’est faux.
D’autres intervalles sont carrément dissonants (7^ème majeure, triton…), la limite entre les 2 groupes n’est pas claire puisque la notion de consonance est relative et subjective et elle a évolué à travers l’Histoire : quelques intervalles peuvent être considérés comme cconsonants ou dissonants selon le gout, l’age, la période, le style, la culture.

Cordes Vibrantes
Si vous grattez une corde (entre 2 points fixes) vous entendez un son d’une certaine fréquence et vous pouvez la voir vibrer, avec des noeuds aux 2 extrêmes et un maximum d’amplitude au milieu. En réalité, la vibration est très complexe, elle est composée de plusieurs vibrations; c’est leur combinaison que vous entendez et vous ne pouvez pas saisir les détails. Le dessin suivant montre les premières courbes de ces vibrations : (en anglais) https://www.youtube.com/watch?v=d0MRsx6oGAg

L’explication est que tout son réel contient plusieurs composantes secondaires de faibles amplitudes et de fréquences multiples qui sont ses harmoniques. En d’autres termes, si vous jouez une note de 100 Hz vous entendrez aussi d’autres plus faibles de 200, 300, 400, 500, 600, etc … Hz (le spectre). Ce fait a été prouvé par le mathématicien français Fourier dans son fameux théorème : Tout signal (électrique, acoustique, etc.), s’il est périodique, peut- être décomposé de manière unique, en un nombre de fonctions sinus dont les fréquences sont multiples de celle du signal.

Harmoniques et Echelle
Appuyons sur la touche Do1 du piano (Do3 est le milieu du clavier), elle produit une suite (infinie, en théorie) de notes dont les fréquences sont multiples de celle de Do1 :

En supposant que la fréquence de Dol est f = 100 Hz (ce qui n’est pas tout-à-fait vrai).
2×f=200 (Do2), 3×f=300 (Sol2), 4×f=400 (Do3), 5×f = 500 (Mi3*), 6×f = 600 (Sol3), 7×f = 700 (Sib3*), 8×f = 800 (Do4), 9×f = 900 (Ré4), 10×f =1000 (Mi4*), 11×f =1100 (X#4**), etc....
* Cette correspondance est rigoureusement vraie en Intonation Juste (IV), mais approximative dans le Tempérament Egal du piano moderne
** Le 11^ème harmonique est exactement à mi-chemin entre F et F# mais ne fait pas partie de l’échelle musicale (occidentale), c’est F≠ de la musique spectrale des années 1970, où le signe ≠ désigne un demi-dièse II.2.
Le fondamental “f” est l’harmonique n°1, 2×f est l’harmonique n°2, 3×f est l’harmonique n°3, etc. Ainsi, les harmoniques ont avec le fondamental les rapports 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, etc. et sont presque tous à l’extérieur de l’octave. Pour les ramener à l’intérieur de l’octave il faut diviser chacun de ces nombres une ou plusieurs fois par 2 jusqu’à obtenir une valeur comprise entre 1 et 2 : 1 pour la tonique Do, Sol est 3/2, Mi (harmonique) 5/4, Sib 7/4, Ré 9/8 (et on ne retrouve pas la quarte).

IV- ECHELLES ET TEMPERAMENTS

1- L’ECHELLE HEPTATONIQUE

L’échelle musicale est une suite de 7 degrés (notes), dont la hauteur (pitch) varie de bas/grave en haut/aigu, selon une disposition bien définie. Elle est qualifiée d’heptatonique mais elle est terminée par une huitième note ayant le même nom que la première, et qui peut commencer une nouvelle suite selon le même format. Cette huitième note résonne très bien avec la première (tonique/racine), c’est l’octave, le rapport de leurs fréquences est 2/1.
Mais, tout d’abord, pourquoi 7 notes, et non pas 9 ou 10 ou 13 ou … ?
Le nombre 7 n’est pas du au hazard, il a été imposé par des critères acoustiques (§2), et confirmé par la Tradition pendant un millénaire en Europe de l’Ouest mais ses origines remontent loin en Histoire au Moyen-Orient (les grecs et les romains avaient une échelle tétracorde à 4 degrés). D’autres nombres existent mais ils dérivent de l’échelle heptatonique : 5 (en supprimant les demi-tons), 12 (en décomposant chaque ton entier), 24 (quarts de tons I.5), 19 (Intonation Juste §4), 31, etc. Plus de 12 degrés par octave l’échelle est qualifiée de microtonale, elle a l’avantage de disposer de suffisamment de notes pour les besoins de “l’Intonation Juste”.
Essayons de créer une échelle musicale, càd un ensemble de sons qui peuvent servir pour composer ou interpréter une mélodie, a priori on peut utiliser tous les sons disponibles dans la Nature, ils sont infinis et certains peuvent ne pas convenir. Vous avez tous remarqué qu’une mélodie transposée une octave plus haut ou plus bas reste identique, ainsi on va se limiter à l’étendue d’une octave. L’octave est l’harmonique qui est juste après la tonique/racine, elle doit donc absolument faire partie de l’échelle (l’hexacorde mediéval n’était pas suffisant).
Imaginons une corde de 60 cm de longueur et tendons-la entre 2 points fixes, sans frettes (c’est le fameux canon/ monocorde). En grattant cette corde elle produit un son avec une fréquence f (par exemple 100 Hz), qu’on va prendre comme référence, et notons la Do (position à vide). L’octave (200 Hz) est située à 30 cm du sillet (figure I.4), càd au milieu de la corde, et limite l’espace sonore qui devrait suffir pour l’échelle (l’octave suivante sera à 45 cm, avec une longueur vibrante 60-45 = 15 cm).
Un autre son/ degré est d’un grand intérêt puisqu’il est très consonant avec la tonique, il correspond à l’harmonique suivant, c’est la dominante. Elle joue un rôle important depuis le début du Plain-Chant (7^ème -8^ème siècle à Byzance), et dans tous les genres/ styles de musique de la planète. N’importe quel musicien débutant peut la repérer facilement, elle est utilisée pour accorder les cordes entre elles (avec l’octave). Elle est désignée par “quinte” parce que, quand l’échelle complète seara achevée, elle occupera le 5^ème rang. Sa longueur est 40cm, càd les 2/3 de 60cm, le rapport de l’intervalle est alors 3/2 en fréquences (sa fréquence est 3/2 × f = 150 Hz).
En suivant ce raisonnement basé sur les Harmoniques on va arriver tout-droit à l’échelle (universelle) heptatonique.

2- ECHELLE DE PYTHAGORE

Nous avons 3 pilliers pour construire une échelle musicale : tonique 1, dominante 3/2, octave 2.
On ne peut pas exploiter davantage l’octave puisque ça ne nous amène à rien de concret : des octaves qui se suivent (même séparées par des quintes) conduisent à des intervalles trop grands, et sans musicalité.
Si vous avez une mélodie pour voix aigue qui commence par la dominante 3/2, l’échelle devra contenir l’intervalle de 3/2 au-dessus de cette note. Son rapport à la première tonique de référence est alors 3/2 × 3/2 = 9/4 (sa fréquence est 100 × 9/4 = 225 Hz), et se situe au-dessus de l’octave 1-2. Pour le ramener à l’intérieur de l’étendue 1-2 on doit le diviser par 2, ça devient 9/4 ÷ 2 = 9/8 = 1,125 ; c’est Ré (voir dessin en bas).
Ainsi de suite, on peut déterminer les rapports des notes suivantes selon la même procédure : à chaque fois on multiplie par 3/2 pour avoir la quinte, et si ça dépasse l’octave on la baisse en divisant par 2. Avec "X" = rapport de X :
Ré→La : "La" = 3/2 "Ré" = 3/2 × 9/8 = 27/16
La→Mi : "Mi" = 3/2 (27/16) = 81/32 > 2 , après réduction : "Mi" = 81/64 .
Mi→Si : "Si" = 3/2 (81/64) = 243/128.
En résumé


Si on continue cette procédure, l’étape suivante est 243/128 × 3/2 = 729/256 = 2,84766 ; en divisant par 2 ça donne 1,42383 . C’est Fa#, qui forme une quarte augmentée (3 tons) avec la tonique (un triton, le diabolus du M-A latin-européen). A ce stade, plusieurs arguments plaident en faveur de Fa plutȏt que Fa# , Fa sera obtenu en descendant d’une quinte à partir de Do, son rapport est 1÷ 3/2 = 2/3. Puisque il est en dessous de la tonique on doit le multiplier par 2 : 2/3 × 2 = 4/3 , comme si on commence le cycle à partir de Fa, càd :
Fa,   Do,   Sol,   Ré,   La,   Mi,   Si
On a alors les 7 touches blanches du clavier.

Remarque
La présence de Fa à la place de Fa# n’est pas facile à expliquer. Probablement des conditions liées à la Culture/ Tradition ont influencé l’audition humaine, dans le sens que la succession de 3 tons (triton) n’est pas appréciée. Par ailleurs, le rapport 4/3 (2 tons et demi, càd Fa) était omniprésent dans la théorie grecque et l’échelle était limitée à 4 notes au lieu de 7 ou 8.

Echelle Diatonique
Le tableau suivant montre les notes de l’échelle, classées selon les rapports croissants, et leurs intervalles exprimés en cents (formule en III.2) :

Le rapport et la distance en cents des 7 degrés sont :

Cette échelle construite sur la base du “Cercle des Quintes” est attribuée en Occident à Pythagore (6^ème A.-J.) bien que le premier document qui présente les chiffres ci-dessus soit un livre d’Al-Kindi (9^ème siècle) [Th, pp131-135].
Remarquons la présence répététive du nombre/rapport 9/8 = 1,125, il définit le “ton” pythagoricien, sa hauteur est :
[log₂(1,125)] × 1200 = 203,9 ≈ 204 cents
Les autres degrés (Mi-Fa et Si-Do), désignés par le terme “limma”, sont assimilés à des demi-tons. Leur valeur de 256/243=1,0535 (ou 90,2≈90 cents) est inférieure légèrement à la moitié d’un ton standard (100 cents).
En confondant limma et demi-ton (comme dans le piano moderne), on obtient le schéma suivant
T    T    ½    T    T    T    ½
C’est le Système Universel, il a été appliqué (par les musiciens) dans des endroits du Monde (Europe, M-O, Inde) très éloignés et sans aucun contact entre eux. Car cette échelle est imposée par la Nature et ses lois/principes, les savants/théoriciens n’ont fait que calculer ses intervalles. L’échelle pentatonique (Chine, Europe Celtique, Afrique) dérive de ce Sysème Universel par suppression des demi-tons.

Le Comma : l’écart entre un ton et 2 limmas [9/8÷(256/243)÷(256/243) = 1,01364] est 203,9 – 180,4 = 23,5 cents (formule en III.2), il est désigné par “comma” (ditonique). Il existe un autre type de comma (§5), leur trait commun est leur hauteur d’environ 22 ou 23 cents qui équivaut grossièrement à un neuvième de ton.

3- CERCLE DES QUINTES

La quinte (suivante) de "Si" aura un rapport de 3/2 × "Si" = 2,84766 . En divisant par 2 on a 1,42383 . Le rapport entre ce nouveau son et Fa est 1,42383 / 1,33333 = 1,06787 . Il est situé approximativement à un demi-ton au-dessus de Fa.
Pour simplifier, on a gardé la même nomenclature et on a ajouté des signes d’altération # qui indiquent d’élever le pitch de la note de 1,06787 (113,7 cents, un peu plus qu’un demi-ton), c’est un apotome. Pour atteindre Sol on doit monter de 203,9 – 113,7 = 90,2 cents, c’est un limma. Nous remarquons que le ton Fa-Sol (ou n’importe quel ton X-Y) est composé d’un apotome (Fa→Fa#=113,7) et d’un limma (Fa#→Sol=90,2), désignés d’habitude par demi-ton chromatique et diatonique respectivement. La différence 113,7 – 90,2 = 23,5 cents est le comma (ditonique), égal à peu-près à la neuvième partie d’un ton, 4/9 pour le limma et 5/9 pour l’apotome.
On peut continuer cette opération en montant par quintes à partir de Fa#, on aboutit à un groupe de 7 notes plus hautes d’environ un demi-ton
Fa → Do → Sol → Ré → La → Mi → Si ====> Fa# → Do# → Sol# → Ré# → La# → Mi# → Si#
L’écart 1,06787 ≈ 1,07 est (légèrement) plus grand qu’un demi-ton standard 1,05946 ≈ 1,06 ; ainsi le couple de notes Mi# et Fa ne sont pas enharmoniques (non plus Si# et Do). Leurs rapports (en relation avec la tonique) sont : "Mi#" = 81/64 × 1,06787 = 1,35152 , "Fa" = 1,33333 , leur propre rapport est "Mi#" / "Fa" = 1,01364 (23,5 cents) càd un comma.
Pour retrouver les bémols on doit faire la démarche inverse en descendant par quintes successives à partir de Fa. Cela mène à la suite :
Fab ← Dob ← Solb ← Réb ← Lab ← Mib ← Sib ← Fa
A partir de Fa, à chaque fois, on divise par 3/2 et si le résultat est inférieur à 1 (tonique) on multiplie par 2 pour revenir à l’intérieur de l’étendue 1-2. Par exemple "Solb" est obtenu en divisant "Do" par (3/2)⁶ et en multipliant par 2⁴ ; "Solb" = 1,40466 est plus basse que "Fa#" 1,42383 par 1,42383 / 1,40466 = 1,01364, càd 1 comma. Fa# et Solb, bien que séparés d’un comma, correspondent à la même touche noire, les touches du piano étant accordées d’une manière différente et plus simple (fin de III.2).

En résumé, pour chaque couple de notes formant un ton entier : X → Y = 203,9 cents

X → X# = 113,7 cents X# → Y = 90,2 cents
X → Yb = 90,2 cents Yb → Y = 113,7 cents
Yb → X# = 23,5 cents
Dans le “Cercle des Quintes” relatif à la théorie de base (I) du Tempérament Egal les notes bémolées et diésées (par ex. Fa# et Solb) sont enharmoniques (et le vrai rapport des quintes est 1,49831 ou 700 cents, très légèrement plus bas que 3/2=1,5 ou 702 cents), c’est ce qu’on apprend à l’école de musique. Le problème est que le TE est relativement récent, et il a été précédé par plusieurs modèles dans le but de réaliser “l’Intonation Juste” (§4).
Examinons la suite des dièses : si on commene par Do pour déterminer les notes de l’échelle diatonique, et on continue à partir de Fa# avec les dièses, la dernière note est Si#, considéré comme identique à Do dans le clavier moderne. Quel est le pitch exact de Si# ? Pour passer de Do à Si# on a parcouru l’étendue de 12 quintes de rapport 3/2 : (3/2)¹² = 129,746 (schéma), alors que ça correspond à 7 octaves de rapport 2/1 : 2⁷ = 128 . Le problème est que ces 2 nombres ne sont pas égaux, Si# est légèrement plus haut que Do :
(3/2)¹² / 2⁷ = 129,746 / 128 = 1,01364 (≈ 23,5 cents)
On peut schématiser cette anomalie par la figure suivante comparant les 2 séries complètes :

Pour remédier à cette situation, on doit baisser Si# pour qu’elle coincide avec Do, dans ce cas, il faudrait réduire chaque quinte du douzième d’un comma, ceci aboutit à la valeur de 1,49831 .

Sinon, on peut utiliser la valeur 3/2=1,5 dans ce schéma circulaire mais il manquerait un comma dont on doit tenir compte, on le note -1 et on le place entre Mib et Sol# (ça ne pose aucun problème puisque ces 2 notes ne se croisent jamais), et 0 ailleurs le long des 11 autres quintes [Th, p87] (§ suivant).

4- INTONATION JUSTE ET MICROTONALITE

La tierce 408 cents de l’échelle ci-dessus n’est pas harmonieuse (ni la tierce du TE). Cette défaillance a été constatée pendant la Renaissance. La cause est expliquée en II.2-3 et III.5, c’est une question d’harmoniques : la quinte est le “second” harmonique après l’octave, l’harmonique suivant est la tierce pure de rapport 5/4 ou 386 cents, plus basse que la pythagorienne d’un comma (407,8 – 386,3 = 23,5). Le souci des théoriciens de la Renaissance était de concevoir des modèles imposant des tierces 5/4.
Cette idée a conduit à plusieurs manières d’accorder les sept degrés, ils sont désignés par “Tempéraments”, et sont qualifiés de “justes”, d’où l’expression “Intonation Juste”, les tons ne sont plus égaux. On connait le nom de Zarlino car son modèle est très simple à exposer (mais pas commode et n’a jamais été exploité) [AC, pp77-81]. Le modèle méso-tonique de Pietro Aaron est plus rigoureux mais il implique certaines procédures arithmétiques. Des corrections ont été ajoutées au modèle méso-tonique initial juqu’à 1800 (et même après) [Th, pp102-105].
Zarlino posa les premières quintes : d’abord Do-Sol, ensuite Sol-Ré et Fa-Do, leur rapport est 1,5 ; ainsi nous avons les 5 notes en gras. Pour compléter l’échelle il a introduit les tierces parfaites 5/4 : Do-Mi, Fa-La, Sol-Si :

Le résultat est une échelle où les tons ne sont pas tous égaux. Do-Ré vaut 9/8 comme avant, et pour Ré-Mi ? La tierce Do-Mi est 5/4, il reste seulement 10/9 (182 cents) pour Ré-Mi : 5/4 ÷ 9/8 = 5/4 × 8/9 = 10/9
Cette échelle (ou mode diatonique) contient 2 sortes de tons : un majeur 204 cents et un mineur 182 cents (en plus du demi-ton). Si on forme les modes chromatiques plusieurs nouveaux intervalles vont apparaitre [Ac, p80], sans parler des enharmoniques distincts (comme Fa# et Solb). Trop compliqué pour les praticiens.
Un autre modèle a été conçu dans le même 16^ème siècle, pour remédier à l’existence de 2 tons différents, il sera appelé méso-tonique (à ton moyen). Puisque l’objectif de l’Intonation Juste est d’introduire la tierce juste 5/4 (en plus de la quinte 3/2), le Mi obtenu après 4 quintes (Do-Sol-Ré-La-Mi, §2) a un rapport de 81/64, et il est plus haut que 5/4 de 81/64 ÷ 5/4 = 81/84 (21,5 cents, comma syntonique). Nous pouvons réduire chacune des 4 quintes d’un quart de comma, d’où l’expression “méso-tonique 1/4”, leur hauteur devient 1,49535 au lieu de 3/2=1,5 (un écart de 3 pour 1000 ou 5 cents qui reste vraiment acceptable). Avec cette valeur de la quinte on peut calculer de nouveau les degrés de l’échelle. On obtient alors 2 sortes de degrés, équivalents à un ton et un demi-ton:

La consonance des quintes et des tierces est acceptable, mais ce modèle a des “défauts”, le plus évident est que la somme de 3 tierces 5/4 n’est pas égale à une octave : 5/4 × 5/4 × 5/4 = 125/64 = 1,9531 < 2 , et l’écart est d’environ un quart de ton (41 cents).
L’étape suivante est de déterminer les notes chromatiques, avec une quinte de 1,49535. La quinte (suivante) de Si est : 1,86919 × 1,49535 = 2,7951 , ou 1,39754 en divisant par 2. C’est Fa#, plus haut que Fa (1,33748) de 1,04487 ou 76 cents.
Le modèle de Pietro Aaron donne des notes bémolées et diésées (par ex. Do# et Réb) assez distantes alors qu’elles “devraient” être enharmoniques.

Chaque ton entier est composé de 3 parties quasi égales, elles peuvent être considérées comme des tiers de ton, et les limmas (Mi-Fa et Si-Do) peuvent être divisés en 2 parties légèrement plus petites qu’un tiers de ton (en posant Mi#=Fab et Si#=Dob). Cela fait 19 degrés ayant tous une valeur comprise entre 58 et 65 cents. Diviser 1200 cents en 19 parties égales donne 63,2 cents, à peu-près un tiers de ton standard : méso-tonique ou 1/3 de tons, les 2 concepts mènent à la même échelle [Th, p104].
Cette solution a eu du succès et plusieurs clavecins et orgues à 19 touches étaient fabriqués durant le 17^ème siècle (et début 18^ème ), même le fameux Zarlino a eu son propre 19 touches :

De nouvelles divisions de l’octave en plus de 12 degrés ont été exploitées pour répondre aux critères de l’Intonation Juste, elles sont appelées “microtonales”. La division par le nombre 19 a acquis un succès certain depuis presque un siècle (Joseph Yasser, Joel Mandelbaum, Neil Haverstick) :
http://www.huygens-fokker.org/docs/bibliography.html
http://organ-au-logis.pagesperso-orange.fr/Pages/Temperam

5- LES TEMPERAMENTS

Les théoriciens ont essayé de corriger les “défauts” du méso-tonique en baissant chaque quinte de 1/5, 1/6 …. de comma. Chaque fois la somme de 3 tierces croit vers 2 (octave), et les supposés “enharmoniques” s’approchent. Finalement l’accordage converge progressivement vers le Tempérament Egal (qui n’est autre que le méso-tonique 1/12 de comma).
Au 17^ème siècle les différents mésotoniques à 19 degrés (1/4, 1/5, 1/6 … de comma) étaient peut-être assez satisfaisants pour les besoins des théoriciens mais les praticiens n’ont pas abandonné le “vieux” clavier duodécimal. Pour simplifier les 19 degrés à 12 il fallait réduire les chromatiques à 5, on n’a gardé que les altérations les plus courantes : Fa#, Do#, Sib, Mib, et Sol# l’a emporté sur Lab car c’est la note sensible de La mineur [Ac, p87]:

Dans le schéma circulaire, rappelez-vous que losqu’on met Si#=Do, il y a un manque d’un comma qu’on répartit (Remarque, fin de I.4) entre les quintes du Cercle, les théoriciens placent ce déficit -1 entre Mib et Sol# [Th, p87]. Le mésotonique ¼ réduit chacune des 11 quintes (de Mib à Sol#) du Cercle d’un quart de comma, ceci mène forcément à +7/4 of comma (presque 2 commas) entre Sol# et Mib : 7(1/4) - 11(1/4) = - 4/4 = -1 . L’intervalle Sol# → Mib est appelé “Quinte des Loups” car elle est trop haute et n’est pas agréable.

Tempérament méso-tonique 1/4

Après de nombreuses tentatives pour réduire la “Quinte des Loups”, les accordeurs ont cherché à répartir le comma syntonique excédentaire entre les touches, selon le désir de chaque musicien. Cependant, les accordeurs ne sont pas tous intéréssés par la théorie et les fractions, et l’accordage devient un art, et l’art n’obéit pas à des règles (Debussy II.1). L’idée la plus répandue, adoptée en particulier par Bach dans son “Clavier bien-tempéré”, était d’accorder la tonalité centrale (avec tierce harmonique) et ses proches voisines au détriment des tonalités lointaines.
Finalement, on a 7 touches blanches diatoniques et 5 noires (Mib, Sib, Fa#, Do#, Sol#). Les quintes sont réduites d’une très petite fraction de comma, et restent assez consonantes. On ajuste/tempère quelques tierces locales (d’une manière empirique) pour être un peu plus consonantes, selon la tonalité de la pièce et le gout du musicien. Un des Tempéraments les plus évoqués est Werckmeister III : la tierce Do-Mi est abaissée de seulement ¾ de comma (la place du 4^ème quart est moins importante).
Tempérament n° III de Werckmeister

Tempérament méso-tonique 1/6 de comma (Silbermann)