[Ac] Histoire de l'Acoustique Musicale



It is a set of sounds, expressed in the form of notes, laid on steps/degrees of a scale. These notes (and others) are used for making music : composing, playing and singing.They begin with a low one (whose frequency is low) which represents the tonic/root and go sharp gradually terminating with the octave which sounds in great harmony with the root. We’ll return later (IV) to the acoustical reasons which have imposed these notes, their number and pitch (pitch being the music term for frequency) and the way they are arranged.
The basic scale contains seven notes (white keys of piano), their names are : C-D-E-F-G-A-B (-C).
The steps are not equal. If we consider the distance in pitch between C and D as a unit, denoted by “tone”, between each note and the succeeding one ( i.e. C-D, D-E, F-G ….. ) the distance is a whole tone except E-F and B-C which are only half a tone or semi-tone (figures above and below).
This heptatonic scale is the reference, but many peoples on earth use a pentatonic scale, by removing the semi-tones (E and B). On the other hand, the division may be extended to12, 19, 24 or more steps to the octave.
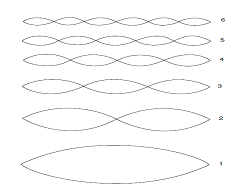
The notes of music (and chant) are expressed by means of several parallel lines grouped in 2 sets, called staves (plural of staff/stave), marked by a particular sign at the left. The most common one is named treble staff; its symbol is G clef. You can see in figure below the tones ˅ and semi-tones ˄ within an octave (notes can be extended to high and low).

The drawing of the piano key-board shows how to divide each tone by inserting a black key, the result is that the total span of the octave is 12 semi-tones, among them only 7 at most are taken to create a melody. These 7 notes form a “mode”, or “key” (although “key” denotes also one element of a piano or organ key-board), or “tonality” (tonality is more related to what is “tonal”, i.e. the style in practice since late 17th century, with prevailing of chords II).
The C note on the ledger low line (under the staff) corresponds to C in the middle of the piano, and the notes above cover roughly the keys on the right. To display low sounds and voices (keys on the left), a second set of parallel lines begins at this C note downwards, it is bass clef :

All over the world, a melody doesn’t use any sounds among the infinite sounds (having whatever frequency) available in nature, but only certain sounds whose number doesn’t exceed 7 and are defined in an accurate way called “mode”. We’ll begin with the basic seven ones, denoted diatonic or natural, provided by the white keys.
The first and most widespread mode (in the West) is shaped after the scale, the ionian/major, it is therefore a reference and a model (with T = whole tone, ½ = semi-tone) :

We can state that the fifth distance/interval (C→G) equals 3 tones and a half (3T ½) and is qualified as just/ perfect, and the third equals 2 tones and is qualified as major.
The second “mode” is the (natural) minor, its pattern is the eolian mode, defined by the succession of 7 notes starting from A :

The fifth A-E of 3 ½ tones is just/perfect (like that in the major) but the third A-C of 1 tone and a half is minor. For reasons relevant to Harmony (II), the 7th degree is raised by a semi-tone, the mode is then qualified as “harmonic minor”.
These are the official 2 modes of the Western culture, inherited from the Renaissance, and transmitted to the American continents and the rest of the World. Nevertheless a third mode exists, it is the phrygian (oriental kurd maqam), with a weak presence (mainly in protestant Germany and orthodox Russia) :

Thus we can conceive 7 modes comprising only the white diatonic keys (they were all used at different degrees until late Renaissance), starting at any note : C (ionian), D (dorian), E (phrygian), …… A (eolian). Locrian B (½ - T - T- ½ - T - T - T) was less used because its fifth is smaller than just/perfect.
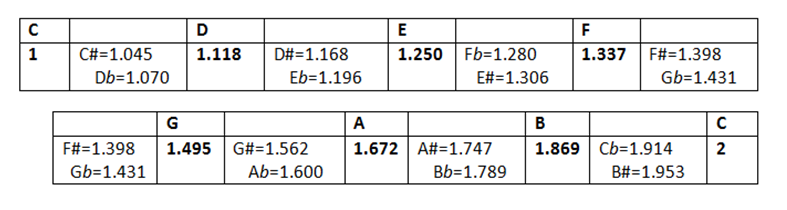
By dividing each of the 5 whole tones we obtain 5 new notes (black keys), they aren’t given any new letters/names but are denoted by signs/ accidentals of 2 types : sharp # to raise the pitch by a semi-tone, and flat b to lower the pitch by a semi-tone. So the 5 black keys are : C# = Db , D# = Eb and F# = Gb , G# = Ab , A# = Bb
If you want, for any reason, to start a major mode at a higher pitch, at G for instance, all the notes should be raised by an interval of 3 ½ tones. So, we should bring alterations/accidentals to notes of the basic scale :

We were bound to raise F by means of a sharp #. Try now to do the same thing, starting this time on F, it will be necessary to lower B with a flat b .

If you want to form a minor mode starting by D or E (with respect to the pattern of A) you’ll be led to flatten B (in D minor) or sharpen F (in E minor).
These alterations that affect some notes in order to modify them and get a different shape of the mode are grouped in the left, just after the key (G or F) and all together are referred to as “Signature”. A 3rd sign serves to cancel the effect of sharps and flats, it is the “natural” : ♮
Remark : A particular mode, hijaz (½ - 3/2 - ½ - T - ½ - T - T), has several names (phrygian dominant , spanish gypsy or tzigan, freygish, andalu or spanish phrygian, indian bhairavi); it is very common in spanish works, remaining from arabo-andalusian culture.

Signatures
Instead of major G-F or minor E-D (above), if we take any one of the seven (or twelve) notes as a tonic, what are the alterations we must bring to obtain a major or minor mode? For instance, what is the signature of G minor? The answer is : 2 flats B, E. The logical method consists of applying the idea presented above i.e. copying the pattern, but it may need some thinking and counting that we can avoid. This same method leads to an easy series of sharps and flats; one has only to keep in mind this series, in both directions :
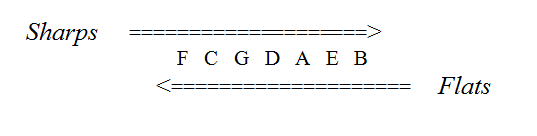
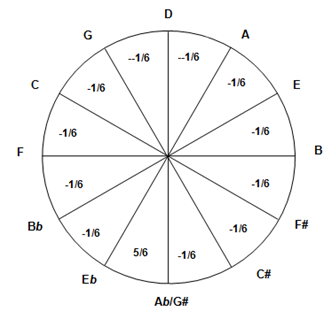
Circle of Fifths (see Remark, end of §4)

This allows us to draw a double-table of major and minor keys :

According to this double-table, Eb major : 3flats, D major : 2 sharps , C minor : 3flats , B minor : 2 sharps, etc.
As for phrygian, starting from a minor mode, we must lower the second degree by half a tone. Example : G minor contains 2 flats, Bb and Eb, we must add the next flat Ab. Thus, the signature of phrygian G is made up of 3 flats : Bb, Eb, Ab
Both modes located on a the same vertical column have the same signature : G major and E minor with 1 sharp, or F major and D minor with 1 flat, i.e. they both use exactly the same 7 notes among the 12 available, and they are called “relative modes”.
We stopped in this double-table at the number 5 accidentals but many authors and professors go till 7 (also few composers in the 19th century), whereas almost all classical as well as modern/popular repertoire doesn’t exceed 3 or 4 accidentals.
The distance between 2 notes is called interval, often it has got a qualifying term which indicates its size (the number of tones inside it). The chart below displays the intervals and their distance to the root :

For any 2 notes X and Y, e.g. D and B, we count from X=1, …. till Y : D=1, then B=6, it is a sixth. It is a major sixth whose size is 4T ½ while E-C = 4T is a minor sixth. We can extend this definition to notes outside the octave.
The octave : 6 tones, the fourth (whatever it is, major or minor) : 2 tones and a half, the fifth in both modes (major or minor) : 3 tones and a half. These 2 degrees, plus the octave, are qualified as just or perfect (P) because their distance doesn’t depend on the type of the mode.
As for the rest of the degrees, their distance depends on the type of the mode, instead of just/perfect they may be major (M), minor (m), augmented (A/aug) or diminished (d/dim). The aug interval has ½ tone more than the perfect (C-G#) or major (C-E#), the dim interval has ½ tone less than perfect (C-Fb) or minor (E-Gb ).
When identifying intervals, the accidentals are first ignored : D-B, Db-B, D#-B, D#-Bb are all sixths even if their values are different. C-F# is an aug fourth and C-Gb is a dim fifth, even if they both have the same size : 3 tones (tritone, known as Diabolus).
Inversion : An interval X-Y may be inverted to become Y-X. If the distance of X-Y is n (for instance D-B, a sixth), the distance of Y-X (B-D) is m so that n+m = 9 or m = 9˗n (B-D is a third). After inversion, major becomes minor and vice versa (dim and aug are inverted as well, and perfect remains perfect).
The cent division
The standard Tone (equal to exact sixth part of the octave) of modern key-board (or fretted guitar) is taken as a unit of intervals for practicing music (modes, solfeggio, chords) : 3 tones ½ for the just/perfect fifth, 2 tones for the major second, 1 tone ½ for the minor second, etc. As for the theorists, who have been studying different tunings (IV) and non-standard intervals (next §), there exists another unit, the cent or the hundredth part of one standard semi-tone : 1 semi-tone = 100 cents.
According to this definition, the octave is 1200 cents, the fourth 500 and the fifth 700 in equal scale/ tuning (see Remark below ) :

Interval Ratio
Since ancient times, theorists (and speculators [Th, pp7-11]) have been expressing the intervals by means of ratios/fractions. These were first applied on archaic instrument with only one string : monocord/ monochord (or canon). The canon is a model or reference which serves to measure. The Greeks in the Antiquity studied the monochord and their purpose was to divide it in order to create several sounds, but this purpose wasn’t realized because their unique instrument the lyra (unlike violin or guitar) was composed of isolated strings not to be divided.
Let’s imagine a string of an instrument, having a length of 60 cm, and let’s tune it as C. By putting a left hand finger (and pressing) at different places on the string we decrease the vibrating part and we can play the notes of the scale : C, D, F, G, etc (figure below).
Try to find and play the octave, and measure the length of the vibrating part, you’ll find 30 cm. The ratio between 60 and 30 is : 60/30 = 2/1 = 2. Try again and play the fifth G : its position is located at 20 cm from the nut, the vibrating part is 40 cm and the ratio is then : 60/40 = 3/2 (or 1.5). For the fourth F it will be 45 cm and the ratio : 60/45 = 4/3. For the rest of notes, you will find a series of fractions whose values vary from 1 to 2 (tonic → octave) and may be expressed as decimals : the sound is getting sharper and the frequency (pitch in music jargon) is increasing till becoming double (details in III ).
The concept of ratios/fractions allows us to study intervals from arithmetical view-point, i.e. the adding and subtracting of intervals. For instance, we’ll make the sum of a fifth 3/2 and a fourth 4/3 (C→G and G→ upper C). By the scientific nature of the relation between intervals and ratios (III.2) we must apply a multiplication, not an addition. It is not correct to write “3/2 + 4/3” and this will not result in an octave (3/2 + 4/3 = 17/6 ≈ 3 >> 2). The right operation is
3/2 × 4/3 = 4/2 = 2
fifth + fourth = octave
Adding intervals in the case above-mentioned is easy and leads to simple fractions (of integer numbers), but in other cases (the octave contains 12 intervals) it may be difficult to carry out. For this reason, theorists are bound to use the “cent” division.
Remark : This concept presumes that the fifth is 3/2 = 1.5 = 1.5000 (and the fourth is 4/3 = 1.3333), whereas the fifths in modern key-board are 1.4983 (table in III.2) and this is the exact value used in the Circle of Fifths §3 and in the Table of the cent division above, it is 3/2 minus (-)1/12 of comma (details in IV).
This Remark may not be important at this stage but it will help understand Chap IV.
Steps (or intervals) smaller than semi-tone have been existing since antique Greece. They were suppressed by benedictine monk D’Arezzo (about 1000 AD) in his writings but they remained in practice until early 14th century. Some innovators (Nicola Vicentino) attempted to relive them in the 16th century but since D’Arezzo theory was governed by a semi-tonal structure. A scale of 19 divisions to the octave was designed in the 16th and survived until the 17th century (IV.4), it matched with 1/3 tone. The quarter-tone will appear in early 20th century in connection with the modern Micro-Tonality [Th, pp200-204] : Alois Haba, Wyschnegradsky, Georgy Rimsky-Korsakov (“The Basis of the Quarter-Tone Musical System”, 1925), etc.
( http://electro-music.com/forum/topic-20747.html ,
https://en.wikipedia.org/wiki/Microtonal_music )
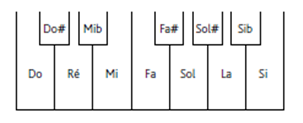
The quarter-tone is present in oriental music. One can rarely find a quarter-tone as a single interval, it almost always serves to form new intervals not existing in western scale, especially 3/4 tone. It is denoted by 2 signs derived from standard accidentals :
Semi-sharp ≠, similar to sharp with only one vertical line, raises the note by quarter-tone. This sign has been used since the 70s in “spectral music” when composers (with scientific background) noticed the presence of F≠ in the series of harmonics (II.2 and III.5). Semi-flat, has several shapes derived from flat, the most common is shown below, it lowers the note by quarter-tone.
Rast is somewhat a reference and a model for oriental modes, it may be considered as a compromise between major and minor (with T = tone, 3/4 = ¾ tone) :

We meet this mode in the afro-american songs of blues and gospel, a “tempered” mode which avoids semi-tones.
There are numerous oriental (arabic, persian, turkish, indian, byzantine) modes (maqams or maqamat in arabic), they haven’t been imposed by theorists (like what happened in the West) but they were set up and have evolved during centuries thanks to great virtuosos. They have their origins in ancient melodies created by musicians, kept alive and improved by generations until being etched on public memory, and finally adopted by theorists. Whereas in the West, theorists of late Renaissance had decreed the prevailing of only major mode, followed by the minor in early Baroque.
There are many tens of oriental modes, exploited in the Near/Middle-East and North Africa, but not at the same degree. Rast and Bayate are the most common, others are rare. So we should classify them into 3 classes : the most common are about 10 (see chart below); follows another list of a dozen less present in the large repertoire accessible to most musicians, and about 20 known only by great professionals and researchers. The point is that some of these modes have got similar genders (first 5 notes) or the same tetracord/ tetrachord since the fifth is usually perfect (3 tones and a half). So it is better counting the genders rather than the modes (for indian modes see [Th, p167]).

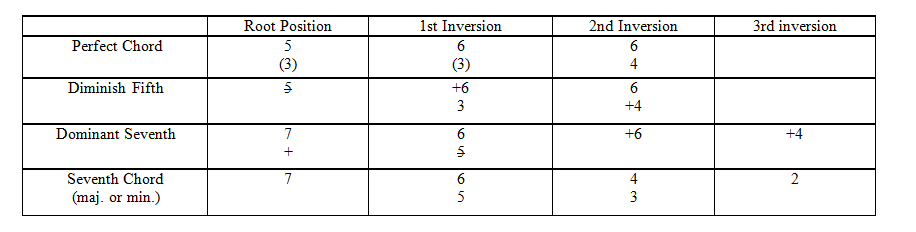
The “triad” is an ancient term that was gradually replaced by “chord” which contains an idea of consonance (II.3) and harmony (although non consonant chords exist). The basic form of a chord is a set of 3 stacked notes i.e. played simultaneously (in a vertical position on the staff) : root, third and perfect fifth, example : C-E-G or A-C-E. The first chord is major since its third (C-E, 2 tones) is major, the second one with a minor third (A-C, 1 tone and a half) is minor. In these 2 cases, the chord is qualified as perfect. Diminish fifth, with 2 minor thirds, is less frequent : B-D-F.

These shapes are conform to the pattern 1-3-5 , but in practice they can be modified by : adding the octave, moving or removing the third, or more generally writing the 3 notes any way as long as the root (C) remains at the bottom (root position) :

Sometimes we add a 4th note (1-3-5-7 : 7th chord), or even a 5th one (1-3-5-7-9 : 9th chord), this gives numerous chords, here are the most common (with Dom = dominant) :

C-E, E-G, G-Bb, Bb-D, this is a succession of (major and minor) thirds. Its shape made some musicologists say that a chord is a series of thirds (tertian/tertial harmony). This point of view is actually wrong, and doesn’t rely on any acoustical argument.
Since the advent of triad/chord in the early Renaissance (about 1400), the purpose was the stacking of notes supposed to be consonant with the root, i.e. pleasant/harmonious when sounding together (II.2-3), they are the harmonics of the root. The problem is that the evolution of music through centuries led to take account of many dissonant “chords” (they have a role to “play” in composition, they must be resolved).
Inversion
When writing different lines or chords in Classical Harmony (II), Baroque composers were often led to “invert” the chord, i.e. change the forward order 1-3-5 and the root is no longer at the bottom. This act allows more choice in the notes to place in each line; in other words, the inversion is not related to any musical/aesthetic fact, it is only a pragmatic method for part-writing :

The resulting shape is not conform to that of triad 1-3-5, i.e. : a bass note, its third and fifth. So, other intervals, like 4th or 6th are formed, and are not harmonious. Rameau wrote on the “scientific aspect” of chords, he claimed that even though we can hear the root but this is wrong (details in [Ac, pp172-173]).
Notation
In Classical and most popular musics, chords are expressed by the writing of the notes that they contain (staff notation), like the examples above and that of II.1, you have only to perform the notes written on the staff. There are other methods of notation which avoid the full writing of notes, and let some freedom to the performers.
The old baroque notation (still in use) consists of putting down the root and complete by numbers which indicate the “quality” of the chord (root position or whatsoever inversion, major or minor …), example in II.4.
Baroque notation :
In modern (of american origin) notation we put the root R and add signs/letters which indicate the “quality” of the chords. So if the root is R : capital R (or RM, or RMaj) for major, small r (or Rm or Rmin) for minor, etc :

If we are inside a known tonality, C major for instance, the chords may be expressed by their rank with roman numerals : capital letters for major and small ones for minor :

Another chord notation used by modern scores, especially in jazz, and supposed to simplify the reading, but it is equivalent to the baroque notation : G7 = G dominant 7th chord in root position, C/E = C major triad in first inversion (E is the bottom), F7/E = F 7th chord in third inversion (E is the bottom).
The score below shows a modern composition in classical (or popular) harmonic style (a simplified passage from “Le Lac” by S. Donval, the famous poem of Lamartine). You can notice 2 staves, treble clef with melody (chant) performed by right hand and bass clef made up of a series of chords F-C-F (I-V-I). One can see/treat this piece either from Harmony or Counterpoint side :

Harmony is the art/technique of combining several lines (voices/parts), or adding chords to a theme line. We are concerned here by “Tonal Harmony”, as it is has been practiced since the Baroque period (more precisely since late 17th century) : a theme and an accompaniment with chords (only in major/ionian or minor/aeolian modes), more details in §4-5.
Centuries before that (late M-A and Renaissance), the Art Music consisted of many voices stacked together to form Polyphony style which flourished during 16th century. The Polyphony is a set of 3 or 4 (or more) melodic lines that must comply with a number of rules referred to as Counterpoint. The upper line (chant or right hand on harpsichord, treble clef) became prominent and the other below lines were grouped in bass clef. Afterwards they were reduced to one line featuring the chords : Figured Bass §4. Harmony has evolved gradually during roughly 3 centuries to become what is known as Common Practice, i.e. the classical or modern style of western music, where the chords and their progression are prevailing. All over this evolution process, the relation between vertical notes have been based on Consonance (euphony/ harmoniousness §3) which is governed by acoustical laws (in the physical sense, III and [Ac]), as we’ll see in the next chapter on “Music Acoustics”.
Music instruments are numerous and different, and each one has its own sound with specific intonation/tone, thus we can distinguish between the instruments even if they play the same note (A3 of Diapason for instance). What makes these sounds different? The answer is that there is no “sounding object” (string, tube, box, etc) which produces a sound with a unique accurate frequency. The main sound (III) is always accompanied by a series of secondary ones having less magnitude/amplitude, their frequencies are multiple of the main frequency. They are called “harmonics” (partials/overtones) and are responsible of making the distinction between sounds; this is referred to as timbre. They are also responsible of Consonance (and Dissonance) which is the heart of Music and its Theory and Harmony.
Let’s take a note whose frequency is, for instance, 100 Hz . If any instrument plays this note, it will also play sounds of (in addition to 100 Hz) : 200, 300, 400, 500, 600, 700 … Hz. This phenomenon is inherent in Nature. The listener hears the stacking of all these partial sounds, they vary according to the "acoustical source", otherwise all people voices will be similar and all instruments will give the same sound (and no need to create new ones).
If we consider C1 (2nd ledger line under bass clef), its harmonics cover the whole Grand Staff, and become very close as they get sharp. They are available in all Theory and Harmony courses. The point is that there is a error in all these writings : the 11th harmonic is presented either as F4 or F4#, but in reality it’s a sound in the middle of these 2 notes, denoted F≠ (≠ is a semi-sharp). The next figure shows the successive harmonics of C1 : C2, G2, C3, E3, G3, Bb3, C4, D4, E4, F≠4, etc.

Some of these partials (if brought inside the octave) match with the degrees of the scale, especially the octave and the fifth. Another partial may be roughly compared with the major third; others are less close (Bb3) or rather far (Ab4) from their correspondings. The reason is that the modern western scale has drifted from the principle on which it was built during the Renaissance (IV), and which was intended to fulfill consonance criteria §3.
The ratios of these partials with the fundamental are : 2, 3, 4, 5, 6, 7, 8, 9, etc and are located above the octave. If we want to bring them inside the octave we must divide them by 2 (one or several times) to obtain a ratio between 1 (tonic) and 2 (octave). The result is : 2/1, 3/2, 5/4, 7/4, 9/8, etc (next §). These ratios denote, in order : octave, fifth, harmonic perfect third, harmonic seventh, major second (instead of ninth).
The most prominent degree of the scale, after the tonic and the octave, is the fifth/dominant ; it is present in all chords (e.g. final cadence). Next comes the third, which created various problems through music history. Dividing the scale in equal degrees (100 cents for each semi-tone) is not justified and has no musical argument (IV.4-5). It gives birth to a major third of 400 cents, higher than the pure/just third 5/4 of 386 cents (formula in III.2). This pure third has been the core of music theory since Renaissance because it offers a very harmonious chord (IV). And for this reason, a division of the scale in 19 degrees (instead of 12) was set up in early Baroque, but it could not survive due to the fact that the keyboard was becoming unpractical, and this idea was abandoned (for the same reason, the 13th century theorist Urmawi had designed a 17 degrees scale whose main feature was a pure third in use in Middle-East until the 19th century when it was discovered by Villoteau who accompanied Napoleon in Egypt [Th, p137-p201]).
All musicians throughout the World are applying the principle of Consonance without paying attention to it. When a violinist or a guitarist wants to tune a string he compares it with its octave or its fifth, because there is a (very) pleasant sensation with these 2 intervals, this phenomenon is called “Consonance”, the opposite is Dissonance. The scientific explanation (III) is that these notes are the first, closest and strongest harmonics of the tonic [Ac, VII].
There is unanimous agreement for the consonance of these 2 degrees, in order, the octave and the dominant. They always have been present in the chord since its advent, and since early Renaissance (about 1400) all Polyphony songs were ended by the 3 notes : root/tonic, fifth, octave (the third will arrive later).
These notes are inside the octave, but there are many others outside the octave that are consonant and which we can find easily. Therefore we must use a piano key-board, and start from a low note (far-left of the key-board) : press (and keep pressing) on the lowest C. There are mainly 2 series of consonant notes : the following C and its successive octaves, the dominant G and its successive octaves, etc.
If you produce a sound having a frequency of 100 Hz you will hear a set of other sounds, its harmonics : 200, 300, 400, 500, 600, 700, 800, 900, 1000, 1100, 1200, etc Hz (staff §2).
- 200, 400, 800, 1600 represent the octaves, since every time we go up an octave the frequency (or the ratio) is doubled.
- 300 represents the twelfth degree or the octave of the dominant, 600 and 1200 are its first and second octaves. If we want to meet the fifth/dominant, its frequency is 300 ÷ 2 = 150; its ratio is 150/100 = 1.5 = 3/2 .
- As for 500, it indicates a sound close to the 17th degree, located 2 octaves above the 3rd. Going down an octave we’ll get the 10th : 500/2 = 250 Hz, going down another octave we’ll get the third : 250/2 = 1.25 = 5/4 . The problem is that this ratio corresponds to 386 cents and differs from the major third (400 cents) of the equal division scale (or ET, equal Tuning/ Temperament) presently in use in western music. The difference is weak (1 comma, IV) but its impact is very significant, as we’ll see further in this course.
The chord, since its triad ancestor, has been written in the form of stacked series of thirds (in its root position), to such a point that most people think that its definition is a series of thirds (it is tertial/tertian Harmony), this is wrong because the underlying idea of chords is the Consonance. What adds to the confusion is the phenomenon of Inversion, much exploited in the West for reasons that have nothing to do with musicality, intonation or perception. It leads to dissonant chords, with fourth and sixth intervals, called artificial chords (in comparison with natural chords having only thirds and fifths).
Octave and fifth are recognized as the most consonant by both performers and theorists, but the error made by ancient theorists has been to include the fourth in the series of consonances. The responsible of this error was not the musicians but the theorists who were monks/ecclesiastics, proponent of 1-4-5 and rarely touched an instrument. In 14th century composers began to trust only aesthetical and acoustical criteria. Therefore they used the triad 1-3-5 but the 4th has kept its importance (with the 5th) instituted by benedictine monk D’Arezzo 3 centuries before that, and remained in Tradition, it will be the cause of the existence of F clef. Another reason is that fourth, with tonic and fifth, are the roots of major chords while the rest of degrees are minor.
The western style music (classical and modern : pop, jazz, sound track) is harmonic, unlike other (oriental) styles which are melodic i.e. they contain only one line/voice (though melodic music has always existed in Western Europe since 12th century troubadours but hasn’t been enough treated/emphasized by the authors [Th, pp65-68]). The presence of chords (and their hierachy) is almost as important as the melody. The “mode” is therefore called “tonality”, by opposition to “modality” of (modal) ancient style of Renaissance.
By definition, Harmony is the art/technique of writing works of several stacked voices/parts and the use of chords in order to ensure better intonation. It appeared in the 17th century, as a consequence of the evolution of Counterpoint (15th and 16th) which was a technique of combining independent melodies and was applied to Polyphony of Renaissance.
Although there are many differences between both of them, Counterpoint and Harmony are 2 stages of evolution of the composition. The first consisted of creating one melody-part and adding other parts with respect of the consonance according to an antique belief (degrees 1,4,5), and the use of ancient modes, musicologists qualify this style as “modal”. As for the second, Classic/Tonal harmonic style exploits the chords, their progression, and their variation so to have alternation between consonant (stable, with calm and rest) and dissonant (instable, with tension) chords.
The tonic chord is omnipresent all along the phrase, often preceded by the dominant chord (as in cadences §5); the phrase must begin and finish with the tonic chord in its root position. These 2 degrees, tonic and fifth, are the most important in composition, and their presence defines the tonality.
The first phase of Harmony appeared in early 17th century : the Figured Bass, it evolved from Renaissance Polyphony (and the technique of Counterpoint) by grouping/mixing the down lines in bass clef while the melody/chant remains in treble clef, it was intended for harpsichord or lute player. The Bass line gradually turned into a progression of chords, each chord was identified by a note under which was written the “Figured Bass” notation : one or two (sometimes three) vertical figures : 5above3 (or only 5) for the root position, 6above3 (or only 6) for the first inversion. The composer indicates only the nature and quality of the chord, e.g. Dominant Seventh G in second inversion (G, B, D, F with D in the bottom) : G +6, then the performer will improvise at his convenience, i.e. will play these notes at any position on the staff, as long as D is the bottom (an example from Couperin, 1700) :

Remark: The “tonal” classical system favors the 3 chords I, V, IV; it is a tradition which dates back to a millennium ago when D’Arezzo instituted the supremacy of these 3 degrees (called tonal notes), but IV has been fallen in lower rank (with other degrees).
In early Renaissance the triad 1-3-5 was fully adopted by musicians and theorists of Polyphony. There was no theme in upper voice/line as in today’s music, the writing consisted of stacked independent melodic lines, their number varies : 2, 3 and more but the norm is 4 whose names from low to high are : Bass, Tenor, Alto, Soprano, each has its own ambitus/range :

At the beginning, the writing often started by the lowest line or “teneur”. Teneur means pillar, or something which holds /bears the whole work, it derives from latin verb “tenir”. Is was the “Cantus Firmus” of ancient authors, in form of an easy chant with long/slow notes.
During Renaissance (16th century), this structure evolved gradually to focus on aesthetics in the upper line in the manner of trouvères’ songs. After a short period of Figured Bass (17th), the composers favored the notion of chords, employing even dissonant ones in order to obtain alternation and better intonation. The result of this evolution is the advent of a new style called Accompanied Melody. This style, which will survive until nowadays, dominates the Art Music orchestra and the keyboard/piano playing : the theme whatever vocal or instrumental in high (G clef) and the chords or accompaniment in low (F clef), and the vertical notes on the same beat must belong to the same chord.
This form based on independent lines (part-writing, or voice leading) was set by rigorist authors, but in practice many composers put the upper line (melody) followed by 2 (or 3) accompaniment lines. This view was very common in secular music (De La Halle 13th, Landini 14th) but musicologists have always disregarded it.
Remark : To ensure the Intonation, a parallel motion is strictly forbidden for eighths and fifths because these 2 intervals are the most consonant, and their succession could lead to monotony (notice that the fourth has been ignored).
Chord Progression
The rules (below) of Harmony concern all music/chant polyphonic works since late 17th, using only major and harmonic minor, with focusing on chords and their progression. The alternation is recommended, between stable/calm chords (which mark the tonality) I and V (plus IV sometimes) on one hand, and unstable/tense (or inverted) chords of degrees such as II and VI on the other hand, the presence of III and VII degrees being weak. We can’t give full arguments to explain all notions because the theory of Harmony has evolved through centuries according to practice, tradition and taste.
Unlike Counterpoint, the role of the chords is important, and they are not arranged in any order, there are some series called progressions : the simplest is (I -) V - I , the very common in classical style is (I -) IV - V - I .
Many different chord progressions have been used in History, depending on the period, region or style, one of the most common in pop/rock is I-V-VI-IV, in “Let it be”
( https://en.wikipedia.org/wiki/List_of_songs_containing_the_I–V–vi–IV_progression ).
Resolution
It is the move from a dissonant chord (or tension) to a consonant one (calm/quietness). Resolution means resolving a difficult/ non-satisfying situation that can’t continue. It obeys to specific conditions explained in all Harmony courses. It may happen in several situations (dissonance, inversion or non-tonal degree) that should move to a “stable situation” i.e. the tonic chord (directly or passing via the dominant), rather in root position (see Leading Note and Cadence).
The inversion creates a real confusion : consonant chords ( I, V or whatever ) when inverted are no longer consonant, since they contain intervals other than 3th and 5th (4th G-C, 6th G-E), thus we must resolve them.
Leading Note
In monodic/melodic music a phrase ends with the tonic preceded by conjunct notes, often with the octave preceded by the seventh at a semi-tone below (or the dominant). This is due to acoustical arguments that we explain in details in the acoustics section (Beating of 2 sounds III.4), they recommend to go up by a semi-tone (or down by a tone, a frequency variation of 10% at most that eliminates the beatings). For this reason, the minor seventh (5 tones) is raised by a sharp to be closer to the octave : this closeness at a semi-tone creates an “attraction” towards the octave which offers a stable situation.
As for the harmonic (polyphonic) music, we need this fact of raising the minor seventh to form the perfect cadence, a kind of resolution which ends the phrase. If the mode is minor A, we raise G to G# to obtain the following chord E-G#-B-D 1-3-5-7 on the dominant V (seventh dominant chord) which precedes the perfect tonic chord in its root position; and this is the best way to end a phrase.
These are 2 reasons (from the same acoustical origin) for raising the seventh degree in minor mode, so we obtain the harmonic minor (A-B-C-D-E-F-G#-A).
Cadence
Monotony in music doesn’t comply with Aesthetic, and a phrase must contain different stages of calm/quietness and tension, and various long or short pauses for dividing the phrase like points and other signs in literal text. These pauses, called “cadence”, are preceded by kinds of special or short progression which contribute to Intonation. There are about four or five of them, their name and adjective may vary slightly with authors. The most important is the perfect/authentic cadence, it is the cause of the creation of harmonic minor. It marks the definitive ending of a phrase : perfect chord 1-3-5 in root position, preceded by perfect 1-3-5 (or seventh 1-3-5-7) dominant chord (see below).
Sometimes, for ending a passage (or for any reason), the composer decides a temporary stop; he may invert the tonic chord. In this case, the cadence doesn’t provide the feeling of a definitive/long stop because the bass note is not the root, it is the imperfect cadence. The plagal cadence consists of succeeding the IV and I chords, the latter in root position; with the IV in place of the V this cadence is less pertinent than the perfect one (plagal means false/fake, not genuine).
There is at least one another sort of cadence ending with the dominant, in its root position, it is named half cadence.
Only the perfect cadence is suitable for a definitive stop from the acoustical view-point (the others are valid, they are set up by Tradition and Aesthetic aspects).
Here are 2 examples of perfect cadence.
In major C :
C(I) : C-E-G , G(V) : G-B-D (or G-B-D-F)
The motion from V to I must be conjunct for all notes except G→C, the reason is relevant to acoustical criteria [Ac] :
B → C, ascending half a tone, required, it allows to get rid of beatings (III.4)
D → C or E, moving by a tone, restful
G → C, in the bass (G in treble clef may stay in place)
F → E , in case of V7

The Modulation
A musical work is rarely written in a unique mode/key, unless it is very short. The main melody (or theme) is composed in a given mode, but very often a changing to another mode is occurred. This latter is very close to the main mode, and the changing is called Modulation. The Modulation is made because of the need of Aesthetic and Intonation.
The secondary theme is written in a relative mode (I.3). It may begin with the dominant (or sub-dominant less often), thus one accidental is added.
Anyway, the changing must obey to some conditions, and usually it passes towards a neighbor mode, which differs by 2 accidentals at most : first to the relative mode (with the same signature), then to the fifth or fourth with 1 extra accidental (and their relative modes). Finally, we may add or suppress 2 extra accidentals (including the leading note). The move from major to minor (or vice-versa) implies 2 extra accidentals (“Jeux Interdits”, Narciso Yepes).
This chapter deals with the acoustical principles that explain the fundamental rules of music theory : scale, chords (inversion, resolution), Harmony and harmonics, etc.
First of all, why is the music scale composed of 7 degrees arranged in a rigid pattern (I.1). Why does the Occident exploit only 2 modes, major and minor, among the many available? Why have western europeans given up quarter-tone and other microtones used by ancient greeks and which survived till Renaissance?
About 2 centuries and a half ago, the division of the music scale has been equalized, that is, all the 12 semi-tones (diatonic as well as chromatic ones) have got the same height/pitch (the exact twelfth part of an octave, or 100 cents, I.4) whereas they were slightly inequal in the baroque period. It is the ET, “Equal” (or Standard) Tuning/ Temperament, but some theorists call it “tempered” Tuning (although there is a nuance between both terms). The modern ET is the consequence of simplifying the tunings of baroque era, and for most people's opinion it is not convenient. The reason is that this Tuning doesn’t offer good harmonious chords due to the (bad) quality of its major thirds (the harmonic third is the most consonant, it is lower by one comma, ninth of a tone, we’ll explain its origin IV). This is why there were in Renaissance many attempts to devise Temperaments with consonant thirds; the most famous is Zarlino’s but the Mean-Tone (IV) had more success. As for the fifth, its Consonance (II.3) has always been accepted as excellent.
Consonance is the common factor between music theory and acoustics, it is the evidence that all musics (western, oriental, indian, chinese, etc.) of the world are based on the same acoustical (in the physical sense) laws. It is also the foundation of the triads/chords because these are supposed to be composed of harmonious notes, and therefore it is the basic concept of Harmony : all the degrees of a chord are derived from the harmonics of the root (except the 11th, not to mention the 13th). The inversion has no musical reason; it leads to dissonant chords, which will be exploited in “Common Practice” music to create alternation and intonation.
The western music theory is very influenced by catholic culture because it was dominated by monks and ecclesiastics, who worked on “musica speculativa” [Th, pp7-11] ancient name of “music theory”, they decreed rules that musicians had to apply. Number of these rules were not conform to acoustical criteria, we must then recognise that the western music has nothing universal. Our purpose is precisely to make the most objective acoustical analysis ever made of music.
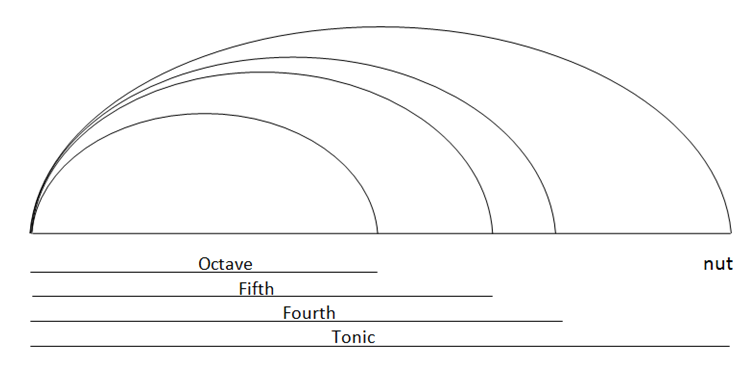
Since Antiquity an equivalence relation has been set up between music intervals and length ratios (ratios of string lengths producing distinct sounds, or distances between holes of wind instruments). Positions of the octave, fifth and fourth are, in order, at : 1/2, 1/3 and 1/4 of the total length of the string, from the nut (figure in I.4). With the help of a graduated ruler one can easily measure the length ratio between 2 positions, and thus deduce the size of the interval between the 2 sounds.
The matter is that untill 17th century authors ignored the nature of sound and the notion of frequency : a sound is the effect of the vibration of a string (or any other “sounding object”) on the ear, after beeing transmitted through the air. If a length l vibrates at a frequency f, a length l’ will vibrate at a frequency f’ so that :
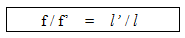
Compared to the open string, you may state that the vibrating lengths of fourth, fifth and octave are : 3/4, 2/3, 1/2; thus the ratios of their frequencies are 4/3, 3/2, 2 and are comprised between the values 1 and 2 (I.4) : the higher the frequency, the shorter the wavelength and the sharper the sound.
Logarithmic Function
The use of logarithmic function is not essential, we can avoid it and use only frequency ratios, but (via the cent system) it can provide us with a regular/linear graduation of the scale of frequencies. Although this logarithmic function is not difficult to handle, its presence may impress people who are not supposed to have scientfic training, its main feature is log (a × b) = log(a)+log(b) for any 2 numbers a and b.
It is convenient to read quantities which are added than quantities which are multiplied, but the nature of some physical notions like sound/loudness makes them non additive, so the Bel and deciBel have been defined by a logarithmic function. The interval (expressed as frequency ratio) also is not an additive quantity, and again logarithmic function is employed.
A musical example, fourth : log(4/3)=0.124939 and fifth : log(3/2)=0.176091, in this case it is decimal log or log10. The sum is 0.124939 + 0.176091 = 0.30103 , this latter number is quite simply log(2) and "2" is the octave.
We saw in I.4 some interval ratios when introducing the cent : it is easy to determine the size in cents of an interval after its ratio, by using the below formula. For the ET we can find the value of the 7 or 12 intervals without passing by this formula. Supposing that all semi-tones are equal to 100 cents, we must calculate x so that x12 = 2, this number x is the 12th root of 2 : 12√2 = 21/12 = 1.0594631 (for a whole tone 1.05946312 = 1.12246). In other words, if you multiply this number 12 times by itself (which is equivalent to add 12 times the same interval/semi-tone) you’ll find "2" .

It is obvious that an accuracy of 5 decimals is not useful for the pratician but it is necessary when we must do several successive theoritical operations. By the way, you should compare these ratios of F and G with those in the end of I.4.
Interval/frequency graduating
Let’s take a real example : F and B; their ratios are : "F"=1.3348, "B"=1.8877 . Their distance is 1.8877÷1.3348 = 1.4142 i.e. the ratio f’/f of their frequencies (or their inverse vibrating lengths) is 1.4142 . What is then the frequency of their middle? It is not the average (in the arithemetic sense) ( f + f’ ) / 2 = ( f + 1.4142 f ) / 2 = 1.2071 × f = 1.6112 but is sqrt (f × f’) = 1.5874 (="G#"="Ab"). Another similar example : 4th + 5th = 8ve , the relation between these 3 ratios is 4/3 × 3/2 = 12/6 = 2 . The difference 3/2 ÷ 4/3 = 9/8 (204 cents) is a (pythagorean) tone. Hence the graduating of the frequency scale must be done in a multiplicative/logaritmic (not additive/linear) way.
Theorists don’t like employing the frequency unit. Instead of expressing the span of an interval between 2 notes by the ratio of their 2 frequencies, they employed the old “savart” unit present in many writings till the mid 20th century, but removed by the “cent”.
The cent is concieved so that the equal/standard semi-tone (either diatonic or chromatic), which is the exact 12th part of the octave, must be equal to100 cents. It is a clear simple unit, convenient and widely adopted nowdays :
I (f,f’) = 1200 × log2 (f’/f) .
This formula divides the span of an octave (one to double) into regular/equal additive parts from "1" if f’=f (0 cent) to "2" if f’ = 2×f (1200 cents).
The first quotation in antique Europe of the concept of lengths ratio and its relation to intervals is mentioned in “Division of the Monochord” or “Division of the Canon”, a book accredited to the famous Euclides (about 300 BC). Probably, the true author is Cleonides, much less known than Euclides but there is a little similarity between both names. A monochord served as a model (canon) to study and determine the length ratios and therefore concieve a musical scale. The 2nd century greco-roman polymath Ptolemy wrote his “Harmonics”, this term has nothing to do with our harmonics/partials but points out the harmonious sight and hearing, and focused on (small) integer ratios to explain consonance. Boethius (about 500 AD) by the end of roman Antiquity was proponent of “superparticular ratios” of the form (n+1)/n = 1 + 1/n (3/2, 4/3, 5/4, 6/5, 7/6, …). Although this theory of simple ratios has survived till nowdays, we are sure that it has no relation with consonance [Ac,VII].
The Middle-Ages are the period that lasts about one millennium, starting from the fall of the Roman Empire (in 476) but the end is not very accurate and usually it varies along the second half of the 15th century. Unlike the Antiquity, the M-A were a period of decadence and ignorance. D’Arezzo (about 1000 AD) “reduced every thing to diatonic and gave the “coup de grâce” to quarter-tones inherited from the greek melody” (Amédée Gastoué, Encyclopédie de la Musique, M-A, p559) and set up the “Hexacord” structure. In 1324-25, Pope Johannes 22 edited the decretal advocating the use of the fourth and the fifth as best consonances (instead of third and fifth, which led to triad 1-3-5).
The Renaissance is a big turning point in the west-european music theory. Due to the hymn of Ramos de Pajera [Th, p 100], the advent of the octave as founding structure replaced the old formalism of hexachord. Despite some attempts such as Nicola Vicentino’s, the theorists abandoned microtones; they decreed the supremacy of major mode (which is a copy of the scale). Later, the minor came back after admitting the consonance of the minor third [Th, pp123-125].
Dominant Seventh chord appeared in Baroque era, the motion to the tonic chord is the evidence of an acoustical fact : the Beatings (§4) and the Resolution which allows to eliminate them (perfect cadence). At the same time, the 19 division of the octave had some succes and many 19 key-boards were built (IV.4).
During the “Century of Enlightment”, scientists brought new and rigorous ideas to solve the failures inherent to the building of musical scale. They emphazised the acoustical aspect of music notes and introduced more consonant degrees in the scale in order to improve Just Intonation (IV). In 1700 Ch. Huygens conceived a 31-tones division [Ac, pp104-109] including the harmonic seventh (present in the seventh chord). J. Sauveur (1653-1716) highlighted that any sound contains several partials/ overtones : a “pure” sound hardly exists. The main undulation/wave is always joined by other ones of multiple frequencies called harmonics. Their relative intensities (magnitudes) give various timbres and thus make the distinction between instruments (and voices). Later, Joseph Fourier (1768-1830) will prove mathemathically that every periodical signal (such as sound vibration) is the combination of a series of pure sine functions.
J. Ph. Rameau (1683-1764) is one of the rarest amid great composers who tried to explain Harmony on scientific basis though he was not scientist. He was influenced by Sauveur and wrote many books where he develops his ideas on Harmony and chords [Ac, pp172-173].
F. Savart (1791-1841), another french scolar with a keen interest in music instruments, invented an apparatus to measure sound frequency, the sonometer. His name was assigned to an interval measuring unit no longer in use.
The german polymath H. von Helmholtz (1821-1894) studied the phenomenon of “resonance” of complex sounds. He analysed the effect of harmonics on the Consonance (§5) but, despite his impressive and long equations and calculations, he found results already known (maybe had he the intention to justify them).
Nowdays, the widespread conviction is that consonant degrees are the nearest harmonics, but many people still believe that the just fourth 4/3 (and even the minor third 6/5) is a harmonic of the root/tonic, this is not true (§5).
One example of a wave is what you see on the surface of quiet water when disturbed by a stone’s throw : waves are created and propagate from the impact point in all directions. Sound is very similar, with air in place of water, so its waves are not visible.
Sound is the sensation produced by the vibrations of a material medium (air, sea-water) on the ear, its eardrum gets the vibrations and transmits them to the brain for analysis (a “mike” operates in a similar way). Their features are :
* magnitude/amplitude/loudness : which indicates the intensity, in Physics and Electronics the audio-level is evaluated by a unit called “Bel” or “deciBel”; human ear can support sounds (or noises) not higher than 100-120 dB.
* the frequency, is the number of vibrations emitted per second. Its official unit adopted by the scientists is the Hertz, or “cycle per second”. The higher the frequency the sharper the sound, maximum span of audible sounds is 20 to 20000 Hz (infra and ultra-sounds are too low or too high for human ear). The band between 40 and 4000 Hz (don’t forget the harmonics) covers the entire 7 octaves of the piano.
* timbre is related to the complexity of the shape of the vibration : a “pure” sound has a sinusoidal graph (fig1 below) and is not pleasant to hear and looks like a whistle. A real sound is composed of a fundamental plus a series of harmonics (the spectre/spectrum, from scientific view-point) with intensities more or less weak; that is the cause of the distinction between sound timbres.
Sinusoidal Form
The curve of sine function is displayed in mathematics by figure 1 :
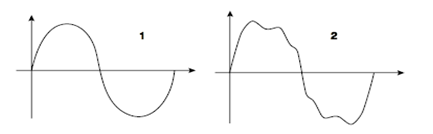
The ordinate vertical Y axis indicates the amplitude (or magnitude) “a” of sine function, and the abscissa horizontal X axis the time “t”.
For the wave on a water-surface, if you look along a radius at a given instant (imagine that you take an overall photo) you’ll see exactly a sinusoidal form. Besides, if you look at a fixed point, e.g. a little floating object, it will go up and down, its position varies in time following a sinusoidal form.
It is evident that an acoustical vibration depends simultaneously on space and time as well. For the sake of simplicity we’ll keep only the time parameter, so the amplitude of the vibration will be expressed in function of time by the formula : a = A sin (2πf × t) . “A” is the maximal amplitude.
The frequency f is the number of cycles/waves in a second. When a sound is said to have a frequency of 100 Hz, this means that the successive waves generated by the plucked string have hit the eardrum 100 times every second.
The duration of one undulation is T = 1s/100 = 0.01 s = 10 ms , it is defined as the period T of the wave :

By definition, a signal or whatsoever event is said to be periodical (or cyclic) if it repeats, identically, regularely, after each invariable time-interval named period (there are numerous examples in Nature and daily life).
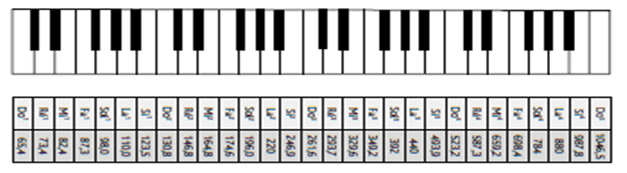
Ancient theorists have always referred to string length in order to study the musical scale in that string-intruments were the most widely used and measuring a length has been very easy, whereas electrical/electronic instruments [Ac, XV-XVI] appeared a century ago (Theremin). The common factor to all these devices is not length, but frequency (Diapason A3 is determined by its frequency of 440 Hz).
Frequencies of the central octaves of piano key-board (ET, Equal/Standard Temperament, [Ac, p16])
Beating of 2 Sounds
Beating is a phenomenon which happens when 2 notes with close frequencies sound simultaneously, it presents a sort of “fluctuations” in magnitude.
Graph n°1 is the “image” of a pure sound in physical/acoustical sense, it is simple and smooth. Any real sound has a graph roughly sinusoidal but distorted to some extent, not smooth, graph n°2. Two different notes, C and G for instance, give a global sound image quite regular/pretty, with same frequency as C, since it is a just/consonant interval. Otherwise, the global sound would be complex and its image would be scrambled.
In the case of 2 pure sounds of very close frequencies f and f’ (a gap less than 10%, i.e. f < f ’ < 1.1×f ), the global sound has a frequency between f and f’ but we can also hear something which resembles a low sound having a variable magnitude (with highs and lows). This fact is referred to by “Beating” (or Interferences, in Physics), and this experiment is easy to carry out by means of 2 instuments not well tuned (by the way it helps tune them together) or between 2 neighbour notes (C and C# of a keyboard).
Let's try to tune the strings of a violin on the basis of a reference n°1 (A3, 440 Hz). To tune sharp E4 n°2, we must find its equivalent/ enharmonic on the reference string, at a length of 1/3 from the nut, this leaves 2/3 of vibrating string for E. The musician will tighten or loosen the E4 string, hearing some “beatings”, untill the 2 strings are well tuned and the beatings are eliminated.
Ancient authors call this a “differential sound” because its frequency is the difference between f and f’. We can prove the existence of the “differential” by mathematical formulas that need backgrounds on sine (and cosine) functions (details in [Ac, pp199-201]) : the result is a unique sound, modulated in amplitude (figure below), with frequency (f+f’)/2. For longtime the nature of “differential” has been debated : Helmholtz was convinced that it was an actual sound whereas Rameau thought that it was a simple illusion and he was rather right.

Sound versus Noise
In the late decades, innovator musicians began to exploit some aspects of “Noise” in their works, but what is the difference between “Sound” and “Noise” ?
Any signal produced by a sound object (wind, string, etc), if it is short, may last less than a second, a tenth of second (.1 s) for example. In case of a note of 440 Hz (Diapason A3), the duration of each vibration, or the period, T is : T = 1/f = 1/440 = 2.273 10-3 s = 2.273 ms ≈ 2.3 ms. In conclusion, .1 s / 2.273 10-3 s = 44, any short signal contains several dozens of waves/sines.
What we call “Noise” is a series of untidy sounds, created by an apparatus which is not, a priori, destined to make sounds, thus it is something whose (intrinsic) nature is not desirable. But if you take one of these sounds composing the noise, and which lasts a little fraction of second, nothing can distinguish it from a signal created by a piano or a violon (except the difference in timbre). The distinction lies only on a psychological level.
Both a noise and a musical sound are composed of signals of same nature (i.e. acoustical vibrations, with harmonics), except that in one case these signals are arranged according to the desire of the musician and are performed by an instrument created for this purpose, whereas in the other case they are disorganized, and above all provided by machines which don’t belong to orchestra. The most surprising is that you can make noise with a piano, by hitting disparate and incoherent notes, not related between them; you’ll see the reaction of your neighborhood.
We have already explained this notion in II.3 : Two notes are consonant if they create a feeling of harmony/euphony, rest and quiet; a phrase is always terminated by a consonance (realized by a perfect tonic chord). There is no physical definition or mathematical formula to express this notion, but some intervals of the mode/scale have been estimated as consonant. That is the origin of chords and their evolution through History.
The octave is a perfect consonance. The feeling created by the octave, with tonic, is due to its frequency which is double of the tonic’s and is contained in the tonic as harmonic n°2. The resulting sound has the tonic as fundamental, the octave does nothing but enhance the second harmonic and slightly modify the timbre. The fifth produces a similar effect but with less degree, because it is the 3rd harmonic; it has allways been ranked just after the octave.
The octave then the fifth are the best ranked, they are qualified as “just/perfect intervals”. Next, historically, comes the fourth though its case is very controversial and most authors think (and write) that is a harmonic, but this is really wrong. Other intervals are virtually dissonant (major 7th, diminish 5th, etc). The limit between both groups is not clear, since the notion of consonance is relative and subjective and has evolved through History : some intervals may be considered as consonant/pleasant or dissonant/unpleasant according to taste, period, style, culture, etc.
vibrating Strings
When you pluck a string (betwen 2 fixed points) you hear a sound of a given frequency “f” and you can see its global vibration, with nodes at both ends and a maximum amplitude at the middle. In reality, the vibration is very complex, and it is composed of many vibrations; what you hear is the stacking of all of them and you can’t see the details. The chart below shows the curves of these vibrations :
https://www.youtube.com/watch?v=d0MRsx6oGAg
The explanation is that any real sound contains several componants that are secondary sounds of weak magnitudes and multiple frequencies, they are its partials/ harmonics/ overtones. In other words, if you play a note of 100 Hz you’ll hear also other (weaker) ones of 200, 300, 400, 500, 600, etc….Hz. (the spectrum). This fact was proved by the french mathematician Fourier in his famous theorem : Every (electrical, acoustical, etc …) signal, if it is periodical, can be decomposed, by a unique way, in a number of sine waves whose frequencies are multiple of the signal’s one. When applied to a vibrating string, this means that the sound you hear is the sum of several harmonics (pure sounds) whose magnitudes can be evaluated by formulas drawn up by Fourier.
Harmonics and Scale
Let’s take the key C1 (C3 is the middle of the piano) and keep on pressing it, we can hear a series (infinite, in theory) of notes whose frequencies are multiple of that of C1 :

By supposing that the frequency of C1 is 100 Hz (which is not actually true), we will hear the following freqencies :
2×f = 200 ( C2), 3×f = 300 (G2), 4×f = 400 (C3), 5×f = 500 (E3*), 6×f = 600 (G3), 7×f = 700 (Bb3*), 8×f = 800 (C4), 9×f = 900 (D4), 10×f = 1000 (E4*), 11×f = 1100 (X4**), etc.
* this is rigorously true only in Just Intonation (IV), but approximate in Equal Temperament of nowdays instruments (piano, guitar, etc.)
** the 11th harmonic is exactly the middle between F and F# but is never shown in a (western) music scale (F≠ in spectral music of the 1970s, the sign ≠ denotes a semi-sharp II.2).
The fundamental “f” is harmonic n°1, 2xf is n°2 harmonic, 3xf is n°3 harmonic, etc …. So the various harmonics have, with the fundamental, the fellowing ratios : 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, etc. and almost all of them are outside the octave. To bring them inside the octave, we must divide each of these numbers by 2, one or several times until getting a value comprised between 1 and 2 : 1 for tonic/root C, G is 3/2, just/harmonic E is 5/4, Bb 7/4, D 9/8.
Musical scale is a series of 7 notes or degrees (or steps), whose pitch varies from low/deep to high/sharp, in a well defined pattern. It is called heptatonic but it is terminated by an eighth note with the same name as the first one, and which may start a new series with the same format. This eighth note (octave) sounds very harmonious with the first one (tonic/root), their frequency ratio is 2/1.
But, first of all, why 7 notes, and not 9 or 10 or 11 or whatever else ?
The number 7 was imposed by acoustical criteria (§2), and confirmed by the Tradition during the last millennium in West Europe but its origins go back far away in History in Middle-East (the Greeks and Latins had a tetrachord scale). Other scale numbers exist but they are derived from the heptatonic one : 5 (by removing the semi-tones), 12 (by dividing each whole-tone), 24 (quarter-tones I.5), 19 (Just Intonantion, §4), 31, etc. More than 12 degrees per octave the scale is qualified as microtonal, and it has the advantage of disposing enough notes for the need of “Just Intonation”.
If we want to build a musical scale (out of nothing), i.e. a set of notes which may be used to compose or perform a melody, a priori we can’t use any sounds available in Nature, they are infinite and maybe some of them will not conviene. All of you have noticed that a melody transposed an octave higher or lower remains identical, so we’ll be limited to the span of an octave.
The octave is also the next and most important harmonic after the tonic/root, so it must absolutely take part of the scale (the medieval hexacord was not suffisient).
We’ll use a string of 60 cm and stretch it between 2 fixed points, without frets (the famous monochord or canon). When plucking this string it produces a sound whose frequency is “f” (e.g. 100 Hz) and is denoted C (open string).
The octave (200 Hz) is situated at 30 cm from the nut (figure in I.4) i.e. middle of the string, and it bounds the sonorous space that should be enough for builing the scale (the next octave will be at 45 cm, with a vibrating length 60-45 =15 cm).
Another note has a great interest because it is very consonant with the tonic and corresponds to the next harmonic. The dominant is an important degree since the beginning of Plain-Chant (around 8th century in Byzance), and in all music styles of the Planet. Any beginner musician can spot it easily, it is used to tune the strings between them (along with the octave). It is denoted by “fifth” because, when the whole scale is achieved, it will be in the 5th rank. Its vibrating length is 40 cm, i.e. the 2/3 of 60 cm, the ratio of the interval is then 3/2 in frequency (its frequency is 3/2 × f = 150 Hz).
This formalism based on Harmonics will lead straight on to the heptatonic scale.
Remark : We have already explained the building of the heptatonic scale by a rigorous method founded on harmonics (II.2 and III.5), with Bb instead of B; untill late Renaissance B was usually flattened (Musica Ficta). But authors and musicologists prefer the method (§2) of the “the Circle of Fifths”, we think the reason is that it leads to a series of 2 diatonic tetrachords (the tetrachord is an old concept inherited from greek Antiquity).
Role of the dominant (fifth)
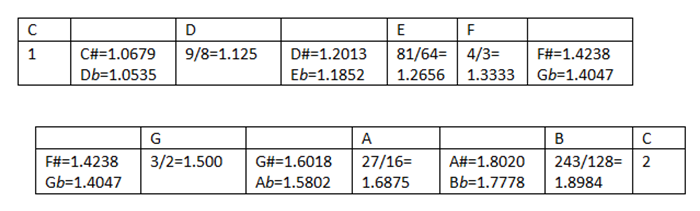
Now we have got 3 pillars to construct a musical scale : tonic 1, dominant 3/2, octave 2. So if your melody or mode/key has this dominant as tonic, the scale should contain an interval of 3/2 ratio of this new tonic. Its ratio to the first/ reference tonic is then : 3/2 × 3/2 = 9/4 (its frequency 9/4 × f = 9/4 × 100 = 225 Hz), it is situated above the octave 1-2 . In order to bring it inside the octave we must divide it by 2, it becomes 9/4 ÷ 2 = 9/8 = 1.125 (it is D, see figure below).
And so on, we can determine the ratios of the following notes using the same process : each time we multiply by 3/2 to get the next fifth, and if it exceeds 2 we must lower it on dividing by 2 . With "X" = ratio of X :
D→A : "A" = 3/2 "D" = 3/2 × 9/8 = 27/16
A→E : "E" = 3/2 (27/16) = 81/32 > 2 , after reduction : "E" = 81/64 .
E→B : "B" = 3/2 (81/64) = 243/128.
To sum up :
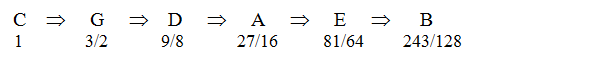

If we continue this process, the next step is 243/128 × 3/2 = 729/256 = 2.84766 , dividing it by 2 will give 1.42383 . It is F#, it forms an augmented fourth (3 tones) with the tonic (it is the tritone, the diabolus of the latin/european M-A). At this stage, several arguments plea in favor of taking F rather than F#, F will be obtained by descending a fifth from C, its ratio is 1÷ 3/2 = 2/3 . Since it is below the tonic we must mutiply it by 2 : 2/3 × 2 = 4/3 (as if we started our Series of Fifths from F instead of C).
So the new shape of the Series of Fifths is :
F, C, G, D, A, E, B
It corresponds to the seven white keys.
Remark : The presence of F instead of F# is not easy to explain. Probably cultural/traditionnal conditions have influenced human hearing in that the Tritone or succession of 3 tones is not appreciated. Besides, the ratio 4/3 (2 tones and a half) was omnipresent in the greek music theory and this fact had great effect on M-A and Renaissance theorists.
Diatonic scale
The following chart shows the notes of the scale, classified by increasing ratios, and their intervals expressed in cents (formula in III.2) :

The ratios of the 7 steps are :

This scale built on the basis of the “Circle of fifths” is credited in the West to Pythagoras (6th BC) though the first document that presents such a method and displays the above ratios is a book of Al-Kindi (9th century) [Th, pp131-135]; we’ll continue to qualify it as pythagorean.
Let’s notice the repetetive number/fraction 9/8 = 1.125 , it defines the pythagorean “Tone”, its height/pitch is :
1200 × [log2(1.125)] = 203.9 ≈ 204 cents
The other steps, E-F and B-C, denoted by the term “leimma” are considered as half a tone or semi-tone. Their value of 256/243=1.0535 (or 90.2≈90 cents) is smaller than the half of a standard tone (100 cents).
If we admit that a leimma may be equal to a semi-tone (like in modern piano key-board), we have the following pattern :
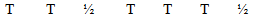
This is a universal system, it has been designed (in practice, by musicians) in places of the World (Europe, M-E, India) far away (and without any contact) from each other. That is because this scale is natural, imposed by the Nature and its laws, scolars have only calculated its intervals. The pentatonic scale (China, Celtic Europe, Africa) is derived from this universal scale by removing the semi-tones.
The Comma : the difference between a tone and 2 leimmas [9/8÷(256/243)÷(256/243) = 1.01364] is 203.9 – 180.4 = 23.5 cents (formula in III.2), it is called “comma”, ditonic/ pythagorean comma. There exists another kind of comma (§4), their common thing is their pitch of about 22 to 23 cents, which equals roughly a ninth part of tone.
The (next) fifth of "B" will have a ratio of 3/2 × "B" = 2.84766 . We divide by 2 and get 1.42383 . The ratio between this new sound and F is 1.42383 / 1.33333 = 1.06787 . It is roughly situated a semi-tone above F.
For the sake of simplicity, we have kept the same nomenclature and added an accidental sign # which indicates to raise the pitch of a note by 1.06787 (113.7 cents, a little more than half a standard tone), it is an apotome. To reach G we must go up by 203.9 - 113.7 = 90.2 cents, it is a leimma. We notice that the tone F-G (or any tone X-Y) is composed of an apotome (F-F# 113.7 and a leimma F#-G 90.2), named usally chromatic and diatonic semi-tone respectively. The difference 113.7 - 90.2 = 23.5 cents is the comma, equal to the ninth part of a tone, 4/9 for the leimma and 5/9 for the apotom.
We continue this process by ascending fifths from F# onwards, we’ll arrive at a group of 7 notes shifted/ higher by about a semi-tone :

The shifting 1.06787 ≈ 1.07 is (slightly) higher than a standard semi-tone 1.05946 ≈ 1.06 , thus the couple of notes E# and F are not enharmonic (neither B# and C). Their ratios (in relation to tonic) are : "E#" = 81/64 × 1.06787 = 1.35152 , "F" = 1.33333, so their own ratio is "E#" / "F" = 1.01364 , 23.5 cents, i.e. a comma.
To find the flats, we must make the reverse process on descending by successive fifthts (ratio 3/2) from F. This leads to the series :
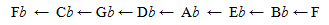
Starting from F, each time we divide the ratio by 3/2, and if it is less than 1 (tonic) we multiply by 2 to bring it into the span 1-2. For instance "Gb" is obtained on dividing "C" = 1 by (3/2)6 and multiplying by 24 , "Gb" = 1.40466 is lower than "F#" 1.42383 by 1.42383 /1.40466 = 1.01364 , i.e. 1 comma. F# and Gb, even shifted by a comma, fit with the same black key; piano keys are tuned in a different way (Table in III.2).
On summarizing, for any couple of notes forming a whole tone : X → Y = 203.9 cents
X → X# = 113.7 cents X# → Y = 90.2 cents
X → Yb = 90.2 cents Yb → Y = 113.7 cents
Yb → X# = 23.5 cents
In the Circle of Fifths related to the basic theory (I) of Equal Tuning flatted and sharped notes (e.g. F# and Gb) are enharmonic (and the ratio of fifths is 1.49831 or 700 cents, very slightly lower than 3/2=1.5 or 702 cents). That is what all music students learn. The point is that the ET is relatively recent, and it was preceded by many models in order to achieve Just Intonation (§4).
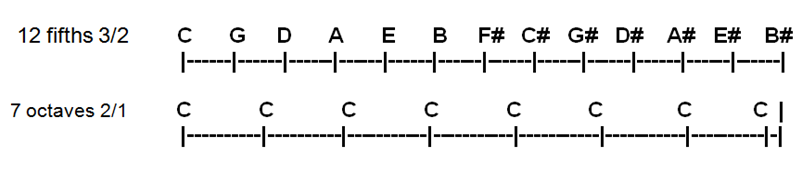
Let’s examine the series of sharps : if you start from C to determine the 7 notes of the diatonic scale, and continue from F to obtain other 7 notes all with sharps, le last note is B#, considered as equal to C in modern key-board. What is the exact pitch of B# ? To pass from C to B# we cover the span of 12 fifths of ratio 3/2, whereas it needs only 7 octaves of ratio 2/1. The global distance in both cases is : (3/2)12 = 129.746 and 27 = 128. The problem is that these 2 numbers are not equal, B# is a little higher than C.
(3/2)12 / 27 = 129.746 / 128 = 1.01364 (≈ 23.5 cents)
We can display this idea by the chart comparing the whole series of fifths and octaves :
If we want to remedy this situation, we must lower B# to match with C, in this case the value of the fifths must be diminished by the 12th of a comma, this leads to 1.49831 .
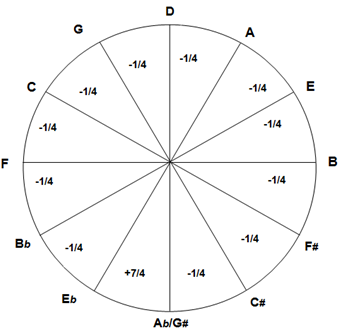
The 12th of comma
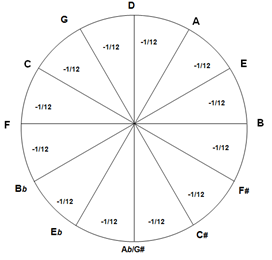
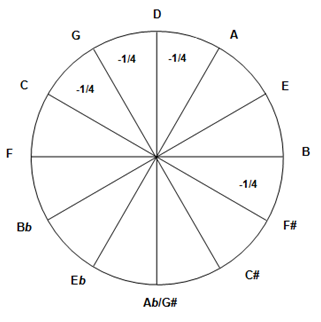
Otherwise we can use a circular chart with fifths of exactly 3/2 = 1.5 , but there is a lack of one comma that we should take into account, usually denoted -1 and placed between Eb and G# (these 2 notes never meet in a mode), and 0 elsewhere along the 11 other fifths [Th, p87].
The third 408 cents of the scale above (§3) doesn’t sound pleasant/harmonious (neither the third 400 cents of the ET). This defect were stated during Renaissance. The cause is explained in II.2-3 and III.5, it is a matter of harmonics : the fifth is "second" harmonic after the octave, the next harmonic is just/pure third of ratio 5/4 or 386 cents, it is lower than pythagorean one by a comma (407.8 - 386.3 = 23.5). The main concern for theorists of late Renaissance was to design models of scales imposing 5/4 thirds.
This idea led to various ways to tune the seven degrees, they are called “Temperament”, and are qualified by “Just Intonation”; the scale has therefore tones which are not equal. People know the name of Zarlino because his model is very simple to display (but is very inconvenient and have never been exploited) [Ac, pp77-81]. The mean-tone of Pietro Aaron is more logical and fulfills acoustical criteria even though it involves some arithmetic operations. Corrections were added to Aaron’s model untill 1800 (maybe later) [Th, pp102-105] .
Zarlino laid the main fifths : first C-G, then G-D and F-C; their ratio is 1.5 , so we have got the 5 heavy-type notes. To complete the scale he added harmonic thirds 5/4 : C-E, F-A, G-B.

The result is a scale where whole tones are not equal. The value of C-D is 9/8 like earlier, but what about D-E ? The third C-E is 5/4, it remains only 10/9 (182 cents) for D-E :
D-E : 5/4 ÷ 9/8 = 5/4 × 8/9 = 10/9
This scale (or diatonic mode) contains 2 kinds of tones : one major 204 cents and one minor 182 cents (in addition to a semi-tone). If we form the chromatic mode many new intervals will appear [Ac, p80]. This could not be accepted by practicians.
Another idea was conceived in the same 16th century, to remedy the existence of 2 different tones, it will be called mean-tone (i.e. middle tone between major and minor).
Since the purpose of “Just Intonation” is to take the just third 5/4 (in addition to the fifth 3/2), the E obtainted after 4 fifths (C-G-D-A-E, §2) has a ratio of 81/64 , and it is higher than 5/4 by
81/64 ÷ 5/4 = 81/84 (21.5 cents, syntonic comma)
We may reduce each of the 4 fifths by a quarter of comma, hence the expression “¼ comma mean-tone”, their pitch becomes 1.49535 instead of 3/2=1.5 (a gap of 3 per 1000 or 5 cents which is really acceptable). With this value of the fifth we can determine again the pitch of the steps of the scale. It has 2 sorts (instead of 3) of steps which are equivalent to tone and semi-tone:

The fifths and thirds may be considered as good, but this model has got some “defects”, the most evident is that the sum of 3 thirds 5/4 doesn’t equal an octave :
5/4 × 5/4 × 5/4 = 125/64 = 1.9531 < 2 , and the gap is about a quarter-tone (41 cents).
The next stage is to determine the chromatic notes (as we did above), with a fifth of 1.49535. The ascending fifth of B : 1.86919 × 1.49535 = 2.7951 , or 1.39754 after dividing by 2. It is F#, higher than F (1.33748) by 1.04487 or 76 cents.
The method of Pietro Aaron gives flat and sharp notes (e.g. C# and Db) rather distant whereas they “should” be enharmonic.
Each whole tone is composed of 3 quasi-equal parts, they can be considered as 1/3 of tone; and the leimmas (E-F and B-C) may be divided into 2 parts slightly smaller than 1/3 tone (by putting E#=Fb and B#=Cb). That makes 19 notes all having a pitch comprised between 58 and 65 cents. Dividing 1200 cents into 19 equal parts gives 63.2 cents, roughly a 1/3 of standard tone : mean-tone or 1/3 tone division, both view-points lead to the same scale [Th, p104].
This solution had some success and many clavichords were built with 19 keys during the 17th (and till early 18th) century, even the famous Zarlino had his own 19 keys :
New divisions of the octave into more than 12 degrees have been exploited to fulfill the criteria of Just Intonation, they are called “microtonal”. The division by number 19 had and still has a notable success (Joseph Yasser, Joel Mandelbaum, Neil Haverstick) :
http://www.huygens-fokker.org/docs/bibliography.html
http://organ-au-logis.pagesperso-orange.fr/Pages/Temperam
Theorists tried to correct the “defects” of the meantone by lowering the fifths 1/5, 1/6 ... of comma. Each time the sum of 3 thirds increases toward 2 (octave), and the supposed “enharmonics” get closer. Finally the tuning converges gradually to the Equal Tuning (which is equivalent to the 1/12 comma mean-tone).
In the 17th the various (19 steps) mean-tone temperaments (1/4, 1/5, 1/6 … of comma) were maybe enough satisfying to respond to the need of theorists but practicians didn’t abandon the “old” duodecimal key-board.
To simplify the 19 steps scale and meet the 12 chromatic one we must remove 7 extra notes, it has been agreed to keep only the most common accidentals : F#, C#, Bb, Eb, and G# was preferred to Ab because it is the leading note of A minor [Ac, p87]:
For the circular display remember that, when we put B#=C, there was a lack of a comma (Remark, end of I.4) dispatched along the fifths of the Circle. Usually theorists place this lack between Eb and G#, it is expressed by : -1 in the circular chart [Th, p87]
The ¼ comma mean-tone reduces each of the 11 fifths (from Eb to G#, clockwise) of the Circle by a quarter of comma, this leads necessarily to +7/4 of comma (near 2 commas) between G# and Eb : 7(1/4) - 11(1/4) = - 4/4 = -1 . The G# → Eb inteval is called “Wolf Fifth” because it is too high and doesn’t sound good.
(1/4) Meane-tone Tuning
After numerous attemps to reduce the “Wolf Fifth”, the tuners sought any empirical way to dispatch the exceeding syntonic comma along the keys, according to the own wish of each musician. Moreover, not all key-board tuners were interested in theory and ratios and the tuning became an art, and the art doesn’t obey to rules (Debussy II.1). The most widespread idea, adopted mainly by Bach in its “Well-Tempered Clavier”, was to tune the main/central tonality (with respect to the harmonic third, in addition to the perfect fifth) and its neighbours at the expense of farther ones.
Finally, we have got 7 white diatonic keys and 5 black keys (Eb, Bb, F#, C#, G#). The fifths are reduced by a very little fraction of a comma, they will be consonant enough. We adjust/temper certain local thirds (in an empirical way) in order to be a little more consonant, according to the tonality of the piece and the taste of the performer. One of the most described Temperament is Werckmeister III : third C-E is lowered by only ¾ of comma (the place of the 4th quarter is less important).
Werckmeister III Tuning
Silbermann tuning is a « 1/6 comma mean-tone »